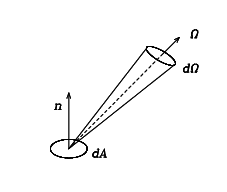
Consider a small area element, dA, from which radiation of frequency n is emerging into a solid angle dW along in a direction at angle q relative to the normal vector [^n] to the surface, in a time dt. We can describe this radiation by a monochromatic intensity, In which is related to the energy En of the radiation by
| (1) |
where the units of the intensity is erg cm-2 sec-1 sr-1 Hz-1. The energy flux, Fn is defined by
| (2) |
and is the quantity of radiation energy passing through the area dA in time dt. It is easy to show by constructing concentric spheres and considering the amount of energy flowing through their surfaces that flux falls of with distance in proportion to the square of the distance, i.e. it follows the inverse square law.
The energy density of the radiation associated with this infinitesimal beam is given by the energy of the beam per unit of distance traveled. Since the radiation travels at the velocity of light, c, the distance dl traveled in time dt is dl = c dt, so that
| (3) |
where dV is the small volume element defined by cosqdA dl.
For a sufficiently small volume element, dV, In is sufficiently close to a constant, and so the energy density of the field un is given by the integral of the intensity over solid angle
| (4) |
The radiation carries momentum, and therefore pressure. The momentum p of a photon is given by p = En/c = hn/c, where h is the Planck constant.
The momentum flux (i.e. the pressure) of In is therefore In/c, and the component of this along the normal to dA is In cosq/c. Further, the flux due to the effective area of dA is dA cosq, so that the pressure of the radiation field normal to dA is
| (5) |
The total pressure along the normal is thus the integral over solid angle,
| (6) |
A useful quantity is the mean intensity Jn of the field, which is the integral of the intensity In over solid angles (i.e. the average In)
| (7) |
In an isotropic radiation field, the flux is the same in all directions. In this case Jn = In. For such a field In is independent of W.
|
and hence that the pressure of the radiation field is related to the energy density by
|
This result can then be integrated over frequency n so that we get
| (10) |

In a physical medium, an infinitesimal beam of light, represented by In travels along a direction l, and will lose energy due to absorption processes (i.e. via its interaction with the matter) and gain energy from emission processes (due to energy production by the matter or by scattering oflight into the beam). Absorption is described by the medium opacity.
Energy may be lost along the beam due to being absorbed by the matter itself, or it may be scattered out of the beam. We can characterise these processes by the opacity of the medium, kn, which in general will be a function of the wavelength, n. This quantity is defined in terms of the mean free path of a photon ln, or the average distance a photon travels along the beam between interactions with the matter.
| (11) |
Alternatively, the opacity of the material can also be expressed as a cross-section, sn, which is defined by
| (12) |
where n is the number density of absorbing particles.
|
|
We now define a dimensionless quantity, tn, which is called the optical depth of the matter. This again will in general depend on the frequency, since matter absorbs radiation with different efficiency at different wavelengths. The optical depth is given by the ratio of the distance traveled ds along the beam relative to the mean free path, and is defined differentially by
| (13) |
The optical depth along a particular direction s tells us about the transparency of the medium, since when tn = 1, the photons are likely to undergo interactions with the medium and do not travel freely within it.
If t >> 1, a medium is termed optically thick, which means that photons will undergo many scatterings within the material. If t << 1, the medium is termed optically thin. Photons traveling through an optically thin medium do so freely and undergo very few interactions with it.
The amount of intensity In removed from the beam along a distance ds is thus
| (14) |
|
|
The matter may also emit photons, adding them to the beam traveling through it. We denote this emission by jn, this being the amount of energy emitted per unit time, per unit frequency, per unit solid angle into some direction, W. Hence the amount of intensity added to a beam dIn is
| (15) |
The change in the intensity dIn of a beam of light along a length ds due to absorption and emission follows from the above and is given by
| (16) |
This is called the equation of radiative transfer. In general, it will depend on the direction W under consideration. The two terms here represent, firstly, the proportional amount removed from the beam, and secondly, the amount of energy emitted into the beam (either via energy generation processes in the material, or by scattering of photons).
An alternative form is obtained by using the definition of the optical depth, dtn = kn ds
| (17) |
where Sn = jn/kn is termed the source function.
This equation describes the radiation field along a beam, which in general is at some angle, q, to the normal to the surface element dA (see figure 6.1). Hence, along some direction of interest, we have the projection onto the normal
| (18) |
where m = cosq.
Multiplying this equation by m and integrating over solid angle dW = sinqdqdf, one can show that the flux Fn obeys
| (19) |
Thus the radiation flux is proportional to the gradient of the radiation pressure.
Photons emitted by a body which is at a constant temperature, T have a particular spectrum (i.e. intensity I as a function of frequency n), which is called the black-body spectrum. The spectral form was calculated by Planck in the 19th century, and is a consequence of assuming that light has a quantum nature. The Planck function is
| (20) |
where h = 6.626 ×10-27 erg s is the Planck constant and k = 1.38 ×10-16 erg K-1 is the Boltzmann constant.
|
|
|
|
For hn/kT << 1, the photons behave like classical particles. In this case
| (22) |
and hence to first order
| (23) |
This is called the Rayleigh-Jeans part of the black-body spectrum.
For hn/kT >> 1, the quantum nature of the photons comes into play. We have
| (24) |
and thus
| (25) |
This part of the black-body spectrum follows the Wien Law, and is seen as a rapid fall-off in the intensity going toward higher frequencies.
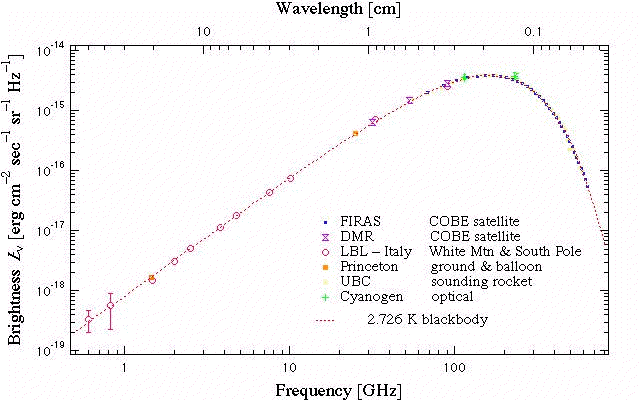
The microwave background radiation, thought to be a relic of the Big Bang, is almost exactly black-body.
The energy density un for black-body radiation is given by
| (26) |
and the pressure Pn of the field (due to photon momentum) is
| (27) |
The total flux integrated over all frequencies is
| (28) |
where x = hn/kT. Performing the integral leads to
| (29) |
and thus the important result emerges that the luminosity L of a body in thermal equilibrium (i.e. at constant temperature) is
| (30) |
The constant of proportionality is called the Stefan-Boltzmann constant, s = 2p5k4/15c2h3 and is 5.67 ×10-5 erg cm-2 K-4 s-1 in cgs units.
For sources which are emitting radiation which is close to a black-body, it is very useful to define the effective temperature Teff, where
| (31) |
One can think of Teff as a ``best fitting'' black body curve to the actual spectrum.
|
plot [1E9:1E22] [1E-40:1E20] to get useful limits on the axes, namely 1 ×109 to 1 ×1022 Hz for the x-axis and 1 ×10-40 to 1 ×1020 for the y-axis. |
For any two blackbody curves, the one with higher temperature has greater intensity than the cooler one for all wavelengths: i.e. a greater flux is emitted at all wavelengths.
Also, as T ® 0, the total flux ® 0,
and, as T ® ¥, the total flux ® ¥.
At what n and l are In and Il maximum?
|
Useful substitutions to make are x = [(hn)/kT] and y = [hc/(lkT)]. (Hint: the first case is equivalent to solving x = 3(1-e-x) and the second case to solving y = 5(1-e-y)). |
The problem above shows that the maximum emission in the black body curve occurs at different places in l and n. Let's denote these l max and n max.
At temperature T, the following relations hold:
|
and
|
In other words n max is a linear function of temperature, T. This simple relationship is called the Wien Law.
|
|
For sources which are emitting radiation which is close to a black-body, it is very useful to define the effective temperature Teff, where
| (32) |
One can think of Teff as a ``best fitting'' black body curve to the actual spectrum.
In the deep stellar interior, the mean-free-path of photons is very short (see problem 6.2), and to a very good approximation the radiation field is isotropic and Planckian with a temperature which corresponds to the local gas temperature. Furthermore, the energy density in the general radiation field is much greater than the general outward energy flux. Let us assume the radiation field is black-body and dependant only on the temperature. The pressure is (as a function of temperature T)
| (33) |
where the outward flux is given by the pressure gradient (i.e. Eq. 6.19)
| (34) |
We can derive the total outward flux, F by integrating
| (35) |
This integral suggests a definition of an average opacity [`k], by
| (36) |
This quantity is called the Rosseland mean opacity.
|
and hence that
where s = ac/4. |
In the context of a star, we are interested in the energy flow outward, and so we associate the path length s with the radius r. Consider the total radiation energy crossing a shell of radius r as having a luminosity L(r). The area of this shell is 4pr2, and the flux crossing it is pF, so that
| (39) |
It is often assumed in stellar interior calculations that the material is in local thermodynamic equilibrium. In LTE, the plasma is assumed to be at or very close to a constant temperature locally. The justification for this assumption is that the mean free path of the photons is typically very small, much smaller than the scale over which the temperature, pressure and density change in the star. The net outward flux of energy is the very small departure of the radiation field from isotropy. The radiation field locally can then be represented to very good precision as Planckian. Having established the intensity of the local radiation field and the temperature of the plasma, the pressure, density and distribution of atomic states may be determined.
The total rate of energy transfer outwards is broadly determined by the temperature gradient, rather than by interactions at specific frequencies, as shown by the luminosity equation (Eq 6.7). This is the reason that Rosseland was able to develop the mean opacity description above.
We have developed equations to describe the flow of radiation, parameterising in terms of the opacity of the material. The absorption and emission of light by the material is ultimately determined by quantum mechanics of the ions or atoms of which it is composed. There are a variety of ways in which an atom can interact with a photon field. Broadly, opacity can be divided into line-opacity and continuous opacity. Line opacity is caused by the absorption of photons by atoms, such as occurs when an electron changes its energy level in the atom, and takes place at specific frequencies. In the outer layers of a star this process results in the familiar ``lines'' in the spectrum. Continuous opacity is of more interest inside the star. Because of the basic physical couplings between photons and ions, photons over a wide range of frequency are able to transfer energy/momentum to the stellar material, rather than at specific frequencies around lines. This is the origin of the term ``continuous''.
For some opacity processes, relatively simple analytical expressions for the frequency dependency can be obtained, in particular for protons, electrons and atoms with only one electron. For more complicated situations, one is forced to attempt detailed numerical calculations of the atomic states of the species, or make use of laboratory data (line lists).
The primary mechanisms which account for opacity are
When a photon collides with an electron initially at rest, the conservation of energy and angular momentum result in the electron being set into motion and a small wavelength change in the photon. For the case of photon energy much less than the rest mass energy of the electron (about 0.5 MeV which is in the X-ray region), the wavelength is increased and the electron gains kinetic energy. For higher energy photons, the wavelength is decreased.
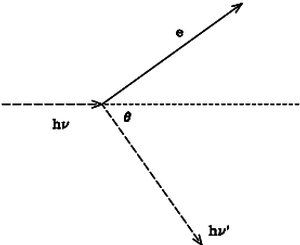
For a photon scattered through an angle q, there is a change in wavelength of 2lc sin2(q/2), where lc = h/me c = 0.024 Å is the Compton wavelength. In the fully relativistic treatment this is known as Compton scattering. The non-relativistic case is called Thomson scattering. A derivation of the cross-section for Thomson scattering sT is beyond the scope of this course, but it can be derived from classical arguments which lead to an estimate of the classical electron radius, re = e2/me c2. The Thomson cross-section is
| (40) |
The optical depth t for Thomson scattering for an ionised gas is
| (41) |
where ne is the electron density.
|
|
In the case that a photon scatters off an electron which is part of an atom, a similiar analysis yields the Raleigh scattering cross-section, sR, and applies when the photon has an energy less than the energy spacings of the atom, DE. Electrons are set into resonant motion along their orbits by the photon, and later re-emits a photon with the same energy (i.e. no change of wavelength) as the first photon. The scattering cross-section is related to the Thomson cross-section by
| (42) |
where hn is the photon energy and hn0 is a measure of the restoring force during the harmonic oscillation. When the photon energy is small (n << n0) we obtain the Raleigh cross-section
| (43) |
The assumption of small photon energy is equivalent to kT << DE, and is valid for temperatures of up to a few 103 K. This process is only important in stellar atmospheres, particularly for cool (late-K and M) stars.
The Thomson cross-section may be used to yield an important limit on the luminosity of a self gravitating body, called the Eddington Limit.
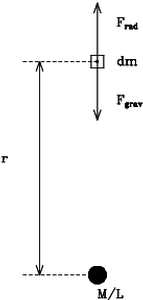
Consider an element of mass m of a cloud of ionised gas, near a luminous object such as a hot star, with a mass to luminosity ratio of (M/L) (see figure 6.4). The radiation force outward on the cloud is
| (44) |
where L is the luminosity of the central source at the cloud and k is the mass absorption coefficient of the cloud, (i.e. the cross section per unit mass) and is defined by kn = kn r.
|
From outward and inward forces on the cloud show that if
then the cloud will be forced away by radiation pressure. |
|
where mH is the mass of the Hydrogen atom. Hence, show that LEdd = 1.25 ×1038 (M/MO) erg s-1, where MO = 2×1033 g. Using the mass and luminosity of the Sun, how close is the Sun to the Eddington limit? |
When an electron moves through an electric field, it experiences an acceleration and radiates photons. In the particular case of free-free or Bremsstrahlung emission, the electron passes thorugh the Coulomb field of a positive ion, typically a proton. As the electron is accelerated during its approach to the ion it radiates photons, and then absorbs photons as it leaves the field of the ion. However, the conservation of momentum and energy mean that in the presence of the ion, these processes do not cancel out, and net absorption or emission takes place.
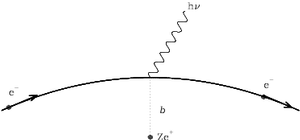
The acceleration acting on the electron as it passes by an ion of total charge Ze+ is of order
| (47) |
and this acceleration acts over a time scale of order Dt = b/v, where v is the velocity of the electron and b is the impact parameter of the collision (distance of closest approach) as shown in figure 6.5. The velocity change due to the acceleration is considered to be very small.
The radiated flux of an accelerated particle with charge e and acceleration dv/dt is given by
| (48) |
and thus the total emitted energy is
| (49) |
Substituting the acceleration dv/dt = Ze2/me b2,
| (50) |
We can also compute the spectrum of emitted radiation, En. As a Fourier series, the emitted flux takes the form
| (51) |
This integral will have non-negligible terms under the condition that 2 pnt » 1 during the time interval of the interaction b/v. Hence, the primary energy emission occurs around the frequency n = v/2bp.
The energy emitted by the electron as Bremsstrahlung radiation can just as well be absorbed by the electron in the field of the ion. This reverse process is then Bremsstrahlung absorption, for which we define a coefficient an, being the absorption (from the surrounding radiation field) per ion per electron of velocity v.
The usual case of interest is that of thermodynamic equilibrium, in which the electron velocities are Maxwellian, i.e. they have a characteristic distribution f(v) which depends only on the temperature T
| (52) |
|
|
In thermodynamic equilibrium, the energy density of the photon field (as shown in an earlier problem) is
| (53) |
so that the total energy absorbed by the electrons from the photon field is the product of the photon flux c un dn, the number density of ions, ni, the number density of electrons, ne, the fraction of electrons with velocity v, f(v)dv and the absorption coefficient, an. For completeness, we note that there is a further factor of (1-e-hn/kT), which takes into account the amount of stimulated emission (the bremsstrahlung re-emitted by the electron as a result of the changes produced during bremsstrahlung absorption).
Under thermal equilibrium, we have the final condition that the absorption and emission fluxes from the electrons must be equal (or their temperature would not be stable) and this allows us to determine the absorption coefficient
| (54) |
Assuming that the velocities of the electrons f(v) are Maxwellian, we can integrate the absorption coefficient over velocity to obtain the thermal bremsstrahlung opacity kff. This can be shown to be of the form
| (55) |
where [`g]ff(n) is the Gaunt factor and is of order unity over a wide range of pressure and density conditions. In general its value has to be computed by numerical rather than analytical methods for the particular conditions under consideration.
|
Using the definition of the Rosseland mean opacity (Equation 6.36) show that
where k0 is a constant and a function of the composition of the star. (Hint: ni and ne are the number of ions and number of electrons in the ionised gas.) |
This form of the opacity is known as Kramer's opacity.
The chemical composition of a star is generally parameterised in terms of the Hydrogen, Helium and heavy metal abundances by mass, X, Y and Z, where heavy metals are all those above Helium in the periodic table.
For stars like the Sun, X » 0.75, Y » 0.23 and Z » 0.02. The chemical composition of the gas after the Big Bang, and before stars began to form was of order X » 0.6 and Y » 0.4, most of the heavy elements having been created by stars subsequently.
|
|
Taking into account the chemical composition of the star, the constant k0 may be written in the form
| (58) |