Module 6

Numerical Integration of Orbits

We looked at two examples of central forces, the central harmonic oscillator and the Keplerian force field.  For both of these cases the orbits can be found exactly (analytically) as a function of time, which is to say that we can solve for the orbit. This is not so in general however. Usually, for any realistic potential field, the orbit is complicated and does not admit of simple or general solutions, even if the potential does not change with time.

The most famous case of a simple system leading to very complicated orbits is called the three-body-problem. Newton solved the two-body-problem (i.e. two point masses moving in their mutual gravitational field), but was unable to solve the three-body-problem. Many people have worked on this problem since Newton, and it is in fact still a very active field even today, three hundred years later! The arrangement of three bodies turns out to be very sensitive to the initial positions and/or velocities of the three bodies and displays what is now known as chaotic behaviour.

In this lecture we will examine the numerical techniques used to solve for orbits when the analytic solution is not known.  This is the way that orbits for spacecraft (such as those that went to the Moon) and stars in the potential field of the Galaxy must be calculated.
 
 

Equations of Motion

The potential is time independent i.e. ∂Φ/∂t = 0.

Let the force (per unit mass) acting on the star be given by F(x,y,z) at the position r(x,y,z) so that

F = −dΦ(r)/dr

In 3-D Cartesian coordinates we can decompose the force into three components F = F(F_x,F_y,F_z), where

F_x = −∂Φ/∂x

F_y = −∂Φ/∂y

F_z = −∂Φ/∂z.

and note that these are partial derivatives.

The equations of motion of the star are (force = mass x acceleration)

d²x/dt² = −∂Φ/∂x,

with similar forms in y and z.
 

Now we will consider a star at the position P(x₀,y₀,z₀) at time t = 0 with velocities (dx₀/dt, dy₀/dt, dz₀/dt) which we denote by (u₀,v₀,w₀).
 

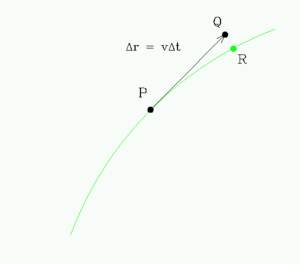The true (unknown) path of the star is shown in green. At P we can use the velocities and position to project the stellar path forward to Q after a time Δt. The actual position of the star after this time is R, and there will always be a small difference (error) between R and Q. In many situations, as we shall see, by choosing Δt small enough one can make this error arbitrarily small, and compute an orbit to any desired accuracy.

To a first approximation, we can compute that the star will move to a new position Q(x₁,y₁,z₁) after a short time Δt based on the velocity of the star at P:

x₁ = x₀ + u₀ Δt

y₁ = y₀ + v₀ Δt

z₁ = z₀ + w₀ Δt.

Furthermore, we can compute the change in the velocities during the interval Δt based on the acceleration due to the force acting on the star at P

u₁ = u₀ + F_xΔt

v₁ = v₀ + F_yΔt

w₁ = w₀ + F_zΔt.

We now have an estimate for the position and velocity of the star at Q. One can repeat (iterate) this procedure to predict the position and velocity of the star as a function of time. Mathematically, this is termed an initial value problem. We solve the equations of motion for a single case by integrating the equations numerically rather than finding the general analytical solution.

The method described above is called Euler's method. A large range of physical problems can be solved using methods based on this technique, and as a consequence a lot of effort has gone into developing fast and accurate versions of the technique; basically, higher order approximations than Euler's linear method are used, and they are known as Runge-Kutta methods. They are much more accurate than the Euler method, which is used here merely to demonstrate the idea. We'll look at those after applying Euler's method to a simple case, simple harmonic motion in 2-D.

Numerical solutions to stellar orbits

Simple Harmonic Oscillator

The simple 2-D harmonic oscillator potential is

Φ(r) = &Omega²r²/2 + const,

and the equation of motion in x is (where r = r(x,y) = sqrt(x² + y²))

d²x/dt² = F_x = −dΦ/dr . dr/dx = −&Omega²r . x/r = −&Omega²x

with a similiar equation in y.

We insert this form into the equations above and solve the equations numerically. The equations in the X-coordinate for the nth step in the integration are:

x_n+1 = x_n + u_nΔt

u_n+1 = u_n − Ω²x_nΔt.

A similar form holds for the y-coordinate.

These equations give us a scheme for "numerically integrating" the orbit. Two examples of the numerical procedure follow, firstly using GNUPLOT and then using QBASIC.
 

Numerical solutions using GNUPLOT

The right hand column column plots out the difference between the exact solution and the numerical solution as a funtion of time, t. You can experiment with using a different number of steps (change imax in the program). This has the effect of making the step size larger or smaller (the step size is denoted by the variable dt. The larger the number of steps the longer the solution takes to compute and the more accurately it matches the analytical solution.

Here are the files:

Numerical solutions QBASIC

Note that using QBASIC is much faster than using the GNUPLOT programs above, but GNUPLOT lets you watch the orbit in real time. Much faster still is to use a compiled language, such as fortran, C, C++, VisualBasic etc. etc. Such languages will compute orbits of this type hundreds of times faster than the interpreted languages which are used here.
 
 

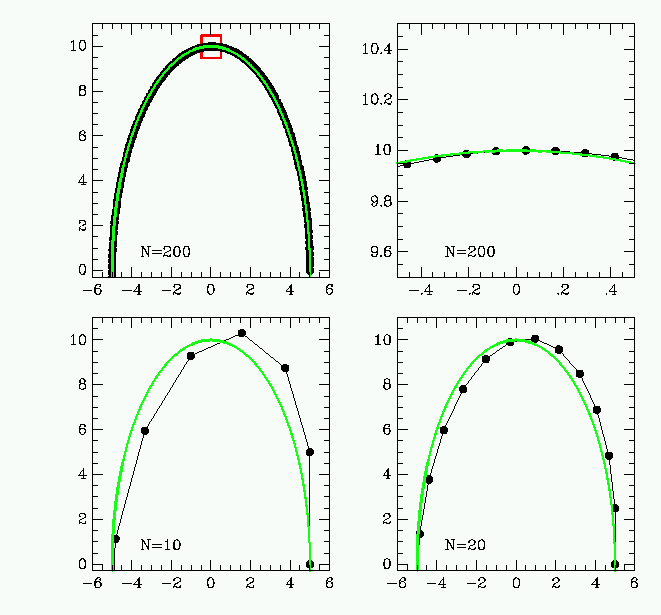
Results of a calculation of a simple harmonic orbit with an exact analytical solution are shown below. The star starts at x=5.0, y=0.0 with velocities u=0.0, v=50.0. The force law is F(r) = −Ω² r with Ω = 5.0. The exact solution is shown by the green line and has the form

x(t) = 5 sin(Ωt+π/2)

y(t) = −10 cos(Ωt+π/2)

The lower left panel shows an iterative solution with 10 steps per time unit (Δt = 0.1), clearly a very poor solution. As N increases to N=20 and N=200 the solutions get closer and closer to the exact solution. The upper right panel shows a zoomed region (indicated by the red box in the upper-left panel), showing that the solution with N=200 is still slightly different to the exact solution.

Runge-Kutta numerical solution

Consider an equation of motion of the form

x'' = f(t,x,x'),

and that we want to solve for x(t) from initial conditions :

x(t₀) = x₀     x'(t₀) = x'₀.

Here, x'' is the 2nd derivative with respect to time t, x' is the first derivative, and the initial position is x₀ and initial velocity is x'₀ at time t = t₀.

Let us expand the position coordinate x as a Taylor series in time, t, for a small step in time, dt.

x(t+dt) = x(t) + dt x'(t) + dt² x''(t)/2 + dt³ x'''(t)/6 + ...

If we retain second order terms only, we get the following approximations:

x(t+dt) = x(t) + dt x'(t) + dt² x''(t)/2
x'(t+dt) = x'(t) + dt x''(t).

Comparison with the Euler method above will show that we have improved it by including all the second order terms. There is actually only one change to be made to the Euler method - the equation which computes the change in the position includes new term, while the equation for the change in the velocity is the same as in the Euler case.

2) Orbits in a Kepler Potential

&Phi(r) = −GM/r

and the force acting at r is

F(r) = −GM/r²

in 3-D cartesian coordinates the force has components F_x, F_y, F_z where

F_x = dΦ/dx . dx/dr = −2GMx/r³

with similiar expressions in the other two components.

Inserting these into Eqns (1) above we derive the numerical form to be solved.

Here is a BASIC program to solve to orbit.
 

Runge-Kutta-Nystrom numerical solution

A yet more accurate integrator is the RKN, or Runge-Kutta-Nystrom method. It extends the (2nd order) RK method above, and is a fourth ourder method, taking into account all terms to dt⁴. From the step n to step n+1, the following quantities are evaluated:

A_n = dt f(t,x_n,x'_n)/2

β_n = dt (x'_n + A_n/2)/2

B_n = dt f(t+dt/2,x_n+β_n,x'_n+A_n)/2

C_n = dt f(t+dt/2,x_n+β_n,x'_n+B_n)/2

δ_n = dt(x'_n + C_n)

D_n = dt f(t+dt,x_n+δ_n,x'_n+2C_n)/2.

This is more general than we need, since the force on the particle depends only on its position, so these reduce to :

A_n = dt f(x_n)/2

β_n = dt (x'_n + A_n/2)/2

B_n = dt f(x_n+β_n)/2

C_n = dt f(x_n+β_n)/2

δ_n = dt(x'_n + C_n)

D_n = dt f(x_n+δ_n)/2.

The steps involved in getting from the from nth step to the (n+1)th step in the integration are:

x_n+1 = x_n + dt (v_n + K_n)

where K_n = (A_n + B_n + C_n)/3

v_n+1 = v_n + J_n

where J_n = (A_n + 2B_n + 2C_n + D_n)/3.