Suomeksi

Determination of latitude and longitude

Nowadays a position anywhere on the Earth can be determined quickly and easily using a relatively cheap GPS receiver. Before the satellite era various radio navigation systems were used. Less than a century ago no such devices were available, and the position had to be found using astronomical observations. In this exercise we try to do the same but without any expensive instruments.

Finding the latitude with the Sun
Finding the latitude with stars
Finding the longitude when the UTC is known
Finding the local time
Finding the longitude when the UTC is not known

1 Finding the latitude with the Sun

The altitude or the vertical separation from the horizon of a celestial object attains its maximum value at the moment it is in South (or in North, depending on the locations of the object and the observer). This event is called the transit. The altitude of the Sun (or any other object) at the moment of transit can be used to determinen the latitude of the observer.

1.1 Observations

The first task is to follow the motion of the Sun on the sky and measure it altitude as a function of time. We start by introducing methods of making these measurements in a very simple and cheap way. They are based on the shadows cast by the Sun.

Method 1:

This method can be used when the Sun doesn't rise very high. This was originally developed for an astronomical exercise in Finland, which lies at a high latitude.

First, find a window through which the Sun will shine during its transit. The window doesn't have to point South; the only important thing is that the Sun is visible through it around noon. Then put a table in front of the window (a window sill might do but it may be too narrow or not exactly horizontal; you should check that with a spirit level). Then you'll need a piece of paper or tin foil, in which you pierce two small holes with a needle. The exact distance of the holes is not important, but you should measure it as precisely as you can. Larger distance will usually give more accurate results. Tape the paper or foil to the window taking care that the holes are aligned exactly vertically. Now the Sun will shine through the holes and there will be two bright spots on the table. To mark the positions of the spots tape a piece of paper on the table.

The transit of the Sun will take place at the local noon. Because our clocks do not show the local time but the time of the nearest time zone, the transit time will differ from 12:00, usually by less than one hour. During the daylight savings time the difference can, however, be almost two hours.

Observations should be started well before the transit of the Sun. In principle we do not know when that will happen, but here we can be a little sloppy and consult an almanac or an astronomical yearbook. Anyway, the Sun will transit around 12 o'clock (or maybe 13 o'clock during daylight savings time). The exact time depends on your position with respect to the parallel of longitude used to determine your official zonal time.

As soon as the light spots hit the paper on the table, mark their positions. It doesn't matter whether you mark the centre or one of the edges, which is easier. What matters is to mark them consistently always in the same manner. Depending on the arrangement you could mark the positions at intervals of a few minutes. The intervals should be pretty accurate, so follow the second hand of your watch. The intervals are important, not the true time. We'll see later how to correct for that.

You will be plotting lots of pairs of points. To keep track of them, draw immediately a line joining the two points belonging to the same instant of time and write the corresponding time next to it.

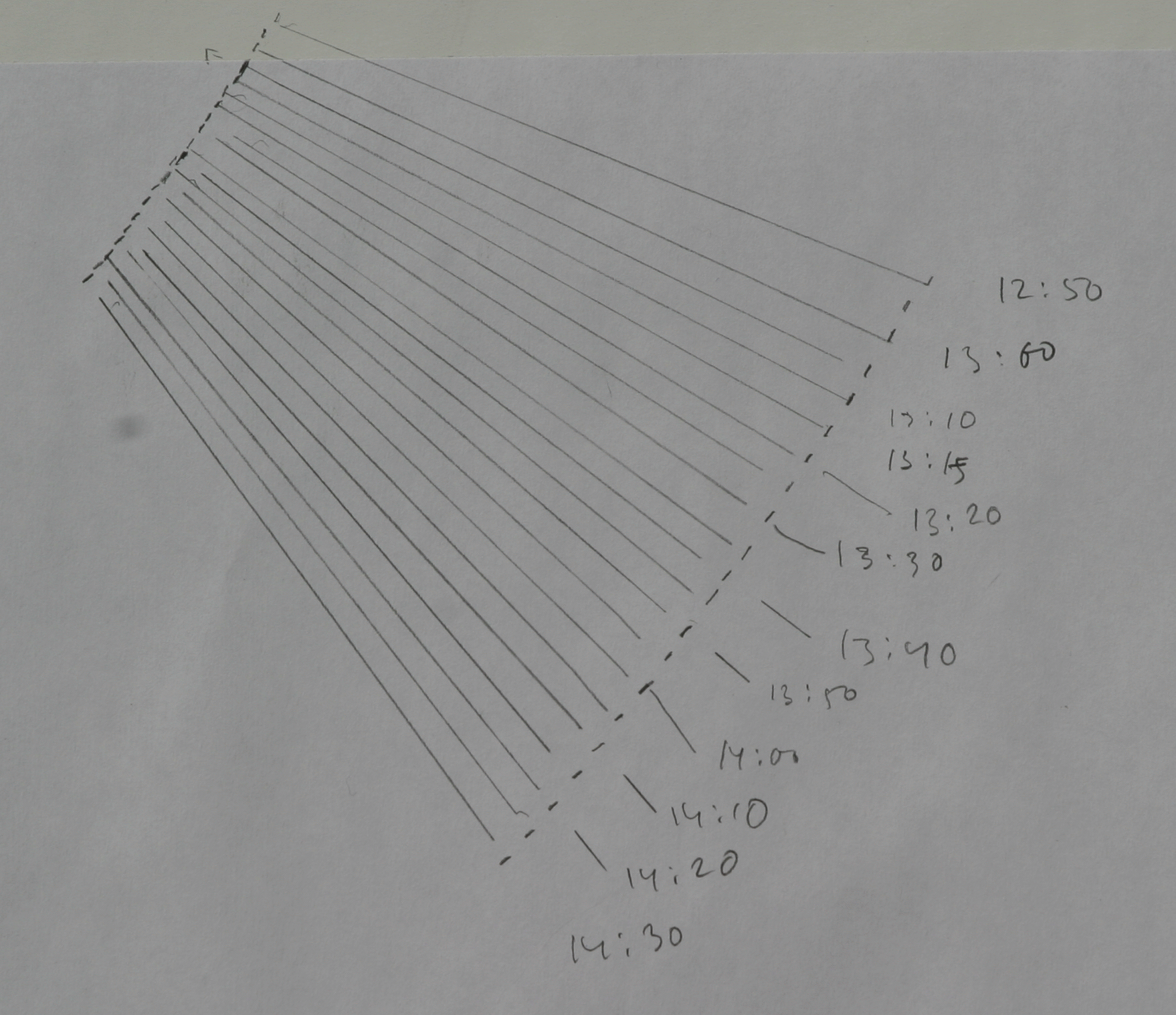
The spots on the paper will approach each other until after the local noon they will begin to diverge. You should continue the observations as long as possible (until the spots move outside the paper).

Now you are ready with the observations. As in most astronomical projects they are just the simple routine part of the work, the tip of the iceberg, so to say. Then comes the analysis, the mathematical part (or the real fun, if you are so inclined).

Practical considerations

In principle the obervations are very simple. In practice you may find out, however, that there are many small details that may ruin the accuracy. When you try the experiment for the first time you will probably encounter the following problems.
Making a nice round hole in a tin foil with a needle is easy. Tiny holes in a piece of paper tend to be irregular and give fuzzy images. The problem with the foil is that it is so very thin and therefore difficult to keep flat on the window. A slightly more complicated but better solution would be to take a piece of cardboard, cut two small openings (about one by one cm, or so), glue the foil to the cardboard, pierce holes in the foil in the middle of the openings, and then press the foil with cardboard against the window glass.
Also the paper on which you mark the light dots should be kept as flat as possible. That is difficult with a big sheet of paper, so again, cardboard is better.
The tiny holes work as pinhole cameras; thus the light dots are actually images of the Sun --- if there are big sunspots they might be visible in the images. Marking the exact centre of the extended image is difficult. It is easier to mark one of the narrow ends of the elliptic image.
The further away the table is from the pinholes the bigger and fainter the solar images will be. To make observations easier it will help to keep the illumination in the room rather dim.

Method 2:

Another method is applicable everywhere, but you have to work outside.

Instead of the pinhole images of the Sun use the shadow of any vertical object (a flagpole, lamppost; or erect a rod just for the measurements). It is important that the shadow is cast on a flat horizontal surface. Also the exact length of the object must be known.

As in the previous method, mark the position of the end of the shadow before and after the local noon at a few minute intervals.

Practical considerations

The higher the pole, the better the accuracy, in principle. However, since the Sun is not a point source, also the shadow will get a lot of light, and the shadow of a tall and thin pole may be very difficult or impossible to detect.
The surface should be smooth. Otherwise the end of the shadow cannot be located unambiguously.

1.2 Calculating the altitude of the Sun

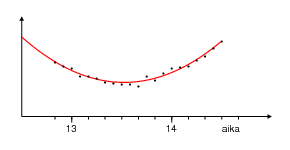
After finishing the observations, measure the distances of each pair of spots or the lengths of the shadow. Plot the results with time on the horizontal axis and distance on the vertical axis. The points should lie on a curve that looks like a parabola. They will not form an exactly smooth curve; there will be some scatter due to small inaccuracies in marking the spots and measuring their distances. Don't worry about this. When there are many observations the small random errors will cancel out. But if there are points that are really a way off, discard them.

Next find the lowest point of the curve; it corresponds to the moment when the Sun reached its highest point on the sky. You can try to draw a smooth parabolic curve approximating the data. If you want to obtain higher accuracy, fit a curve to the data using a least squares method; a small C program for doing the calculations is included. To use the program you have to write the time-distance pairs in a file. The program will calculate a second degree curve describing the data and write the equation of the curve and the coordinates of its apex. See the program file for more details.

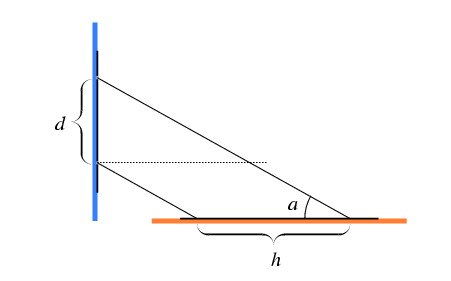
If the distance between the holes in the paper on the window is d and the shortest distance between the light spots h, the maximum altitude of the Sun was

a = arctan d/h.

The same formula applies, if d is the length of the pole casting the shadow and h the length of the shortest shadow.

1.3 Finding the coordinates of the Sun

Next we have to know the position of the Sun on the celestial sphere. The coordinate corresponding to the latitude is called declination. Since the Sun moves with respect to the celestial sphere, its declination keeps changing. The change is fastest during vernal and autumnal equinoxes, about 0.4 degrees a day. During winter and summer solstices the motion in declination stops and reverses its direction.

Method 1:
The solar coordinates at one day intervals at 0 UTC are found here. The columns are: year, month, day, right ascension in hours, declination in degrees, transit time in UTC at the Greenwich meridian.

The declination corresponding to the time nearest to your observations can be used as a rough approximation. A more precise value can be found by interpolation.

Method 2:
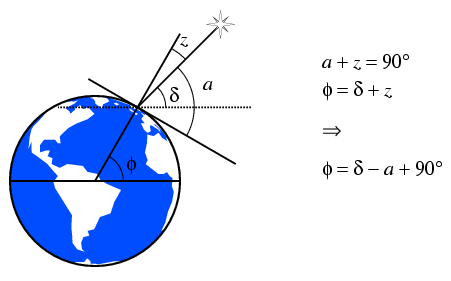
You can find the source code of a small C program here. The program computes the coordinates of the Sun for any moment of time; hence there is no need for interpolation. The precision, however, is not quite as high as in the tabulated values that are based on JPL ephemerides.

1.3 Finding the latitude

Now we know the altitude a and declination d of the Sun. The figure below shows that they are related to the latitude f of the observing site by

f = d - a+ 90\deg.

2 Finding the latitude with stars

Stars are too faint to be observed in a similar way. To use stars, you will need a sextant or some other device for measuring angles. However, they are pretty expensive. With a sextant an experienced observer can reach an accuracy of about 10 seconds of arc, which corresponds to a couple of hundred meters. Coordinate dials of most small telescopes cannot be read that accurately, and such instruments cannot be used for precise latitude determination.

Altitudes are now obtained directly, and can be plotted as before. The highest point of the cureve can be estimated graphically or using a least squares method as before.

Declinations of stars remain fairly constant, and so they can be looked up in a star catalogue. Again, high precision means extra work. Catalogues usually give coordinates for the year 2000. They change slowly mainly due to the precessional motion of the rotation axis of the Earth. Depending on the accuracy required also other, smaller effects may have to be taken into account. The details are somewhat too complicated to be discussed here. If you are interested, consult any textbook on spherical astronomy.

3 Finding the longitude when the UTC is known

Now the latitude is known, and from the same observations we also get the transit time of the Sun. This time can be used to calculate the longitude.

The longitude is proportional to the difference of the local time and UTC. Local time can be determined by observing the transit time of the Sun or any other object the coordinates of which are known. The main problem is that the direction to the South is not known exactly. A compass cannot be used since it is not very accurate and may suffer from unknown perturbations. The previously described method is one way to solve the problem. It is essential to make several observations before and after the transit, and also plot the data. It is not sufficient just to follow the altitude, since at the time of the transit the altitude does not change, and even close to the transit the changes are very small, which makes it difficult to find the maximum precisely. When the curve is plotted, it is symmetric with respect to the instant of transit, and can be used to determine the time with high accuracy, preferably using a least squares program.

For the observations the clock doesn't have to show exactly correct time, since only the time intervals are important. To calculate the longitude, however, the time must be known as exactly as possible. Compare the clock used in the observations to a time signal e.g. on a radio or to some other clock that is known to be very accurate. Using this time difference you can correct the time of the transit. The time signal tells probably the time of your time zone that usually differs from the UTC by an integer number of hours. Find your time zone and use it to calculate the UTC of the transit.

The time difference to 12 o'clock UTC would give the longitude if the transit of the Sun took place at 12 o'clock local time every day. Unfortunately the apparent motion of the Sun is not quite even. We can see this in the last column of the solar table giving the transit time in Greenwich. During the year the transit time moves around 12:00.

Instead of subtracting 12 from the local time, find the transit time in Greenwich and subtract it from the local time. The difference gives the distance from the zero meridian in time units.

Since one full revolution, 360 degrees, corresponds to 24 hours, one hour corresponds to 15 degrees. Multiply the time difference by 15 to get your longitude in degrees.

If the transit took place before 12:00 UTC, the site is East of Greenwich, if after, the site is West of Greenwich.

The rotation period of the Earth is 24*60 = 1440 minutes. Thus an error of one minute in the transit time will mean an error of about 40000/1440 = 28 kilometers on the equator. Therefore you should be as careful as possible with time determinations.

Getting a reasonably accurate latitude is not too difficult. Since the altitude of the Sun changes only slowly, it is much harder to determine the exact time of the maximum altitude. Thus the error in the longitude will usually be much larger.

4 Finding the local time

We can use the observations to determine also the local time.

Example: On March 1, 2009, the transit time is 12.2053 hours and the difference from 12 is 0.2053 hours (12 min 19 sec). This is also approximately the transit time at our observing site (not exactly, since the deviation changes with time, but here we don't care). Thus at the transit time was also 12.2053. If the observed transit time was 14:30, our watch is 14.5000-12.2053 = 2.2947 hours ahead of the local time.

Later you can use this correction to find the local time of any other event. Or, even better, you can adjust your clock so that it will show the local time directly.

5 Finding the longitude when the UTC is not known

Finding the longitude is based on measuring the difference between the local time and the time of some fixed reference place. The problem was very difficult before radio and accurate clocks. The old pendulum clocks did not work well on a rolling boat. The marine chronometre invented by Harrison finally solved the problem. A different solution, suggested already by Galileo, is to use celestial events for which the UTC is known.

The four Galilean satellites of Jupiter have been used for this purpose. The method is quite accurate and simple on solid ground, but on a boat making proper observations is difficult.

To see the Galilean satellites you will need binoculars or a telescope. When a satellite orbits Jupiter it goes through Jupiter's shadow ands seem to disappear. Depending on the relative positions of the Earth and Jupiter it is possible to observe either the beginning or end of the eclipse, but not both. Since the orbital periods of the Galilean satellites are relatively short (Io 1.769 days, Europa 3.551 d, Ganymede 7.155 d, and Callisto 16.689 d), the eclipses are quite frequent.

Times of these events in UTC for the year 2009 are found in a table here.

In 2009 Jupiter is behind the Sun and therefore invisible at the end of January. Therefore the table gives only the events taking place after late spring when observations are possible.

Now the only thing to do is to observe an event, record its local time, and look up the UTC in the table. The time difference in hours, multiplied by 15, gives the longitude as before.

The theory of motion of the Galilean satellites is quite challenging, and different versions give slightly different values. Times given in different sources may vary even by a couple of minutes. Thus you should not be too disappointed if the longitude is not very accurate.