Integraalilaskentaa

Määrätty integraali

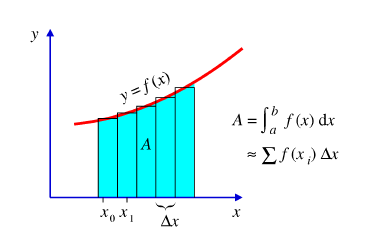
Integraalin arvo saadaan, kun tässä välin pituuden Delta x annetaan lähestyä nollaa. Yhteenlaskettavien kaistaleiden lukumäärä kasvaa samalla rajatta, mutta niiden pinta-alat pienenevät. Jos yhtenlaskettu pinta-ala lähestyy jotakin raja-arvoa, funktio on integroituva.

A = F (b) - F (a),

missä F on alkuperäisen funktion f integraalifunktio. Se on funktio, jonka derivaatta on f:

d F (x)/dx = f (x)

Jos funktio F toteuttaa tämän vaatimuksen, samoin tekee F + C, missä C on mikä tahansa vakio, sillä vakion derivaatta on nolla. Integraalifunktio ei siten ole yksikäsitteinen. Tämä ei kuitenkaan vaikuta määrätyn integraalin arvoihin, sillä vähennyslaskussa F (b) - F (a) vakion arvot kumoavat toisensa.

Seuraavassa taulukossa on lueteltu joitakin integraalifunktioita. Integraalifunktion etsimiseen ei ole samanlaisia yleispäteviä sääntöjä kuin derivointiin. Lopputulos voidaan aina tarkistaa kokeilemalla, onko integraalifunktion derivaatta = alkuperäinen funktio.

f (x)	F (x)
1 / x	ln x
xn	xn+1 / (n + 1)
ax	ax / ln a
ex	ex
ln x	x ln x - x
sin x	- cos x
cos x	sin x
tan x	- ln cos x

I = \int_A f dA

voidaan laskea kaksinkertaisena integraalina lausumalla pinta-alkio dA koordinaattien differentiaalien avulla. Esimerkiksi suorakulmaisessa koordinaatistossa on

dA = dx dy

ja napakoordinaatistossa

dA = r dr d phi.

Ensiksi laskettavan integraalin integroimisrajat saattavat olla toisen muuttujan funktioita.

Esimerkiksi funktion xe^y integraali ylläolevan kuvan alueen yli on

I = \int_A xe^y dA = \int_x=0¹ \int_y=0^2xxe^y dx dy
= \int₀¹ [ | ₀^2x xe^y ] dx = \int₀¹ (xe^2x-x) dx
= |₀¹ (1/2)xe^2x - (1/4)e^2x - (1/2)x² = (1/4)(e² - 1).

Pinnan ei tarvitse olla tasossa. Esimerkiksi pallon pinta-ala on

A = \int_S dS,

missä integrointi suoritetaan pallon pinnan S yli. Tällöin pinta-alkio on

dS = R² cos \theta d\phi d\theta,

ja pinta-ala on

A = \int_\phi=0^2\pi \int_{\theta=-\pi/2}^\pi/2 R² cos \theta d\phi d\theta
= \int₀^2\pi [ | _-\pi/2^\pi/2 R² sin \theta ] d\phi
=\ int₀^2\pi 2R² d\phi = 4\pi R².

Vastaavasti avaruusintegraali

I=\int_V f dV

voidaan laskea kolminkertaisena integraalina. Tilavuuselementti dV on suorakulmaisessa koordinaatistossa

dV = dx dy dz,

sylinterikoordinaatistossa

dV = r dr d\phi dz

ja pallokoordinaatistossa

dV = r² cos \theta dr d\phi d\theta

(tai r² sin \theta dr d\phi d\theta riippuen siitä, mitataanko kulma \theta xy-tasosta vai z-akselista).

Esimerkiksi R-säteisen pallon tilavuus on

V = \int_V dV
= \int_r=0^R \int_\phi=0^2\pi \int_{\theta=-\pi/2}^\pi/2 r² cos \theta dr d\phi d\theta
= \int₀^R \int₀^2\pi [ | _-\pi/2^\pi/2 r² sin\theta ] dr d\phi
= \int₀^R \int₀^2\pi 2r² dr d\phi
= \int₀^R 4\pi r² dr
= | ₀^R 4\pi r³/3
= (4/3)\pi R³.