| kotisivu |
| hakemisto |
| kartat |
| kohteet |
| teoriaa |
| matematiikkaa |
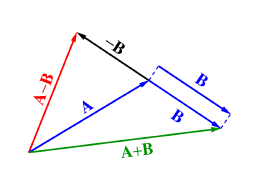
Vektorien A ja B summa voidaan määrätä graafisesti siirtämällä esimerkiksi B:n alkupää A:n kärkeen ja yhdistämällä A:n alkupää B:n kärkeen.
Vektorin A vastavektori -A on yhtä pitkä kuin A, mutta vastakkaissuuntainen. Erotuksella A-B tarkoitetaan summaa A+(-B).

Vektorien yhteenlasku toteuttaa tavanomaiset laskusäännöt
A+B = B+A,
A+(B+C) = (A+B)+C.
Suorakulmaisen koordinaatiston kutakin pistettä (x, y, z) vastaa yksikäsitteinen paikkavektori, joka on vektori origosta ko. pisteeseen. Kantavektorit i, j ja k ovat koordinaattiakselin suuntaisia yksikön pituisia vektoreita eli yksikkövektoreita. Pistettä (x, y, z) vastaava paikkavektori r voidaan lausua muodossa
r = xi + yj + zk.
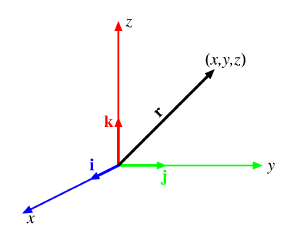
Lukuja x, y ja z sanotaan r:n komponenteiksi. Vektorit voidaan laskea yhteen laskemalla yhteen vastaavat komponentit. Jos esim.
A = axi +
ayj +
azk,
B = bxi +
byj +
bzk,
on
A + B = (ax+bx) i + (ay+by) j + (az+bz) k.
Vektorin r pituus komponenttien avulla lausuttuna on
r = | r | = (x2 +y2 + z2)1/2.
Vektorien A ja B skalaaritulo on reaaliluku (skalaari)
A . B = axbx + ayby + azbz = | A | | B | cos [A,B],
missä [A,B] on vektorien välinen kulma. Skalaaritulon arvo on esim. A:n pituus kerrottuna B:n projektiolla A:n suuntaan.
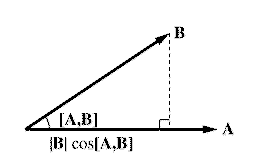
Jos A ja B ovat kohtisuorassa toisiaan vastaan, on A . B = 0. Myös käänteinen tulos pitää paikkansa: jos A . B = 0, vektorit A ja B ovat kohtisuorassa toisiaan vastaan.
Vektorin pituus skalaaritulon avulla lausuttuna on
| A | = (A . A)1/2.
Vektorien A ja B vektoritulo on vektori
A × B =
(aybz -
azby) i +
(azbx -
axbz) j +
(axby -
aybx) k
= det [ i j k ;
ax ay az ;
bx by bz ].
Tämä on kohtisuorassa sekä A:ta että B:tä vastaan. Sen pituus ilmoittaa A:n ja B:n virittämän suunnikkaan alan. Yhdensuuntaisten vektorien vektoritulo on 0.
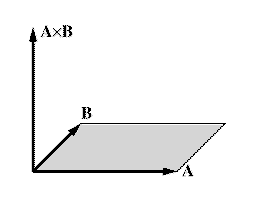
Kaksi vektoria määrää tason: elleivät vektorit ole yhdensuuntaisia, on olemassa yksi taso, joka sisältää molemmat vektorit. Tämä voidaan ymmärtää niin, että kaksi vektoria tulee määrätyiksi, kun annetaan kolme pistettä: vektorien yhteinen alkupiste ja kummankin kärki. Näiden kolmen pisteen kautta voidaan asettaa täsmälleen yksi taso. Vektoritulo on vektori, joka on kohtisuorassa tätä tasoa vastaan.
Vektoritulo poikkeaa tavallisesta kertolaskusta. Jos tekijöiden järjestys vaihdetaan, myös tulon merkki vaihtuu. Vektoritulo on siis antikommutatiivinen:
A × B = -B × A.
Vektoritulon tekijät määräävät tason; tätä tasoa vastaan kohtisuora vektori voi osoittaa kahteen vastakkaiseen suuntaan (tason "ylä- tai alapuolelle"). Tekijöiden järjestyksestä riippuen vektoritulo antaa jommankumman näistä vektoreista.
Sekä skalaari- että vektoritulo toteuttavat tavanomaiset osittelulait:
A . (B+C) =
A . B+A . C
A × (B+C) =
A × B+A × C
(A+B) . C =
A . C+B . C
(A+B) × C =
A × C+B × C
Skalaarikolmitulo on skalaari
A × B . C =
ax (by cz -
bz cy) +
ay (bz cx -
bx cz) +
az (bx cy -
by cz) =
det [ ax ay az ;
bx by bz ;
cx cy cz ].
Tässä pisteen ja ristin saa vaihtaa keskenään ja tekijöitä saa permutoida syklisesti tulon muuttumatta. Esimerkiksi
A × B . C = B × C . A = B . C × A,
mutta
A × B . C = -B × A . C.
Vektorikolmitulo on vektori, joka voidaan laskea kaavoista
A × (B × C)
= B(A . C) - C(A . B),
(A × B) × C
= B(A . C) - A(B . C),
Kaikissa erilaisissa tuloissa voi skalaaritekijöitä siirrellä vapaasti, esimerkiksi
A . kB = k(A . B),
A × (B × kC) =
k(A × (B × C)),
jne.
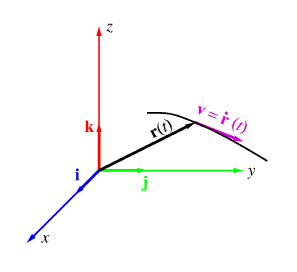
Mekaniikassa kappaleen paikkavektori on ajan funktio
r = r(t) = x(t)i + y(t)j + z(t)k.
Sen nopeus on vektori, joka saadaan derivoimalla r ajan suhteen:
v = dr(t)/dt = = i dx(t)/dt + j dy(t)/dt + k dz(t)/dt.
Vastaavasti kiihtyvyys on r:n toinen derivaatta ajan suhteen d2r/dt2.
Tulon derivointi noudattaa samoja sääntöjä kuin tavallisten reaalifunktioiden tulon derivointi:
d(A . B)/dt =
dA/dt . B + A . dB/dt,
d(A × B)/dt =
dA/dt × B + A × dB/dt.
Vektorituloja derivoitaessa on muistettava huolehtia oikean järjestyksen säilymisestä, koska tulon merkki muuttuu, jos tekijöiden järjestys vaihtuu.