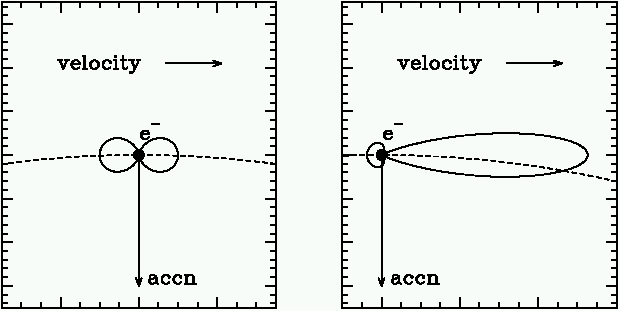
A charged particle moving in a magnetic field radiates energy. At non-relativistic velocities, this results in cyclotron radiation while at relativistic velocities it results in synchrotron radiation. This latter is a very important source of radiation in astrophysics.
The relativistic form of the equation of motion of a particle in a magnetic field is
| (1) |
where v is the velocity vector of a particle of charge q, the magnetic and electric vectors are B and E, m is the mass, and g is the usual Lorentz factor.
Since the force on the particle is perpendicular to the motion, the magnetic field cannot do work on the particle, and so its speed does not change, i.e. |v| = constant. The particle has constant speed v, but its direction may change. Eqn 4.1 can thus be written
| (2) |
Now consider the directions perpendicular and parallel to the magnetic field B. Let v have components v^ and v|| along these directions. Then
| (3) |
and
| (4) |
Eqn 4.3 gives | v|| | = constant and eqn 4.4 gives |v^ | = constant (since v^ ×B. is perpendicular to v).
The motion is very simple; it is uniform and circular around the field lines of the magnetic field B. If the velocity along the field lines is non-zero, then the particle moves in a helical path along the field.
Eqn 4.4 gives the acceleration of the particle, which may be related to the centrifugal acceleration:
| (5) |
where r is the radius of the orbit around the field lines, and is called the ``radius of gyration'', and a is the so-called ``pitch angle'' or the inclination of the velocity vector to the magnetic field lines. For motion perpendicular to the fields, a = p/2.
Consider that the particle is an electron of charge e and mass me, and the acceleration is denoted a.
|
Problem 4.1 Show that the electron acceleration is given by
where b = v/c. Show that the radius of gyration r is given by
Show that the period of gyration P is given by
and that the frequency of gyration, wB, is given by
|
The total emitted power for a relativistic particle of charge q under an acceleration a is
| (10) |
which turns out to be larger by a factor of g4 than the power emitted in the non-relativistic case (i.e Larmor's formula in Lecture 3)
| (11) |
The relativistic version of the Larmor formula follows from considering the power produced in the frame of the particle (for which Larmor's formula applies) and then transforming to the laboratory frame using the Lorentz tranformations.
|
Problem 4.2 Show that radiation emission for a relativistic electron moving in a magnetic field B is given by
where b^ = v^/c and r0 = e2/me c2 is a quantity called the classical electron radius.
|
Eqn 4.12 is the power emitted by an electron moving in a magnetic field and producing synchrotron radiation.
Consider relativistic electrons with isotropically distributed velocity vectors (i.e. they have a velocity directed with equal probability in all directions). Denote the angle between a given velocity vector and the magnetic field line by a, which is termed the pitch angle. Then
| (13) |
and averaging b^ over all pitch angles a, we get
| (14) |
|
Problem 4.3 Show that the total power, Piso, for an isotropic distribution of synchrotron emitting particles is
where sT = 8 pr02 / 3 is the Thomson cross-section and UB is the magnetic energy density of the field, UB = B2/8p.
|
The power emitted by an accelerated particle has a characteristic two-lobe distribution around the direction of the acceleration, illustrated in Fig 4.1. The dependence of the power emitted P, on the angle relative to the direction of the acceleration, q is given by
| (16) |
Synchrotron emission is strongly beamed along the direction of motion, which turns out to be perpendicular to the acceleration. Relativistic boosting of the power takes place along the direction of motion by a factor g2, and the effect of this is illustrated in Figure 4.1. The emission is concentrated into an angle along the direction of motion of order 1/g.

|
Problem 4.4 The relativistic abberation formula relates the angle a¢ at which radiation is emitted by an accelarated charge to its direction of motion and in its own frame, to the angle a, which an external observer measures between the emission and the direction of motion.
Show that at 99.9% of the speed of light :
|
The beaming of the radiation has a very important effect on the observed spectrum emitted by the electron. As the electron cycles around the helical path along the magnetic field line, any emission directed toward a distant observer is seen only when the beam is aligned with the observer's line-of-sight. In this case the observer sees a ``flash'' of radiation for a period which is much shorter than the gyration period. For non-relativistic motion, the gyration frequency wB gives the frequency of the emitted radiation directly,
| (18) |
whereas, in the synchrotron case the characteristic frequency of the emission is at a critical frequency nc, where
| (19) |
A detailed analysis shows that the peak emission is actually at
| (20) |
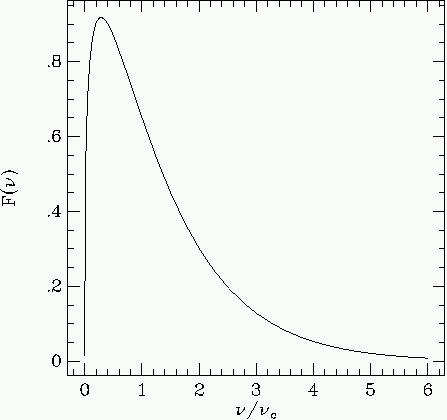
The overall spectrum of the emission consists of the sum of a large number of harmonics of the basic cyclotron emission. The summed spectrum is relatively peaked, with maximum emission at 0.29 nc, and with intensity I(n) dropping like (see figure 4.2).
| (21) |
| (22) |
The electrons in a plasma emitting synchrotron radiation are cooling down. The time scale for this to occur is given by the energy of the electrons divided by the rate at which they are radiating away their energy. The energy E is
| (23) |
and the synchrotron radiation rate is given by Eqn 4.12
| (24) |
Hence, the cooling time of the electrons, t is given by
| (25) |
A further useful result is that at frequency n, the Lorentz factor is given by
| (26) |
The Crab is an approximately 900 year old supernova remnant. The supernova explosion was seen by Chinese astronomers on July 4th, 1054, and was so bright it could be seen by day. It was described by them as a ``guest star''. It was visible for about a month by day and for about two years at night. The Messier number for the Crab is M1 (the Messier catalog is a list of about 100 faint ``fuzzy'' objects noted by the great French astronomer and comet hunter, Messier). Images of the crab now are shown in figures 4.3, 4.4 and 4.5.
Some historical information on the crab is at http://oposite.stsci.edu/pubinfo/PR/1996/22/PR.html



The crab was the first radio source to be identified with an optical object (other than the Sun), by Bolton in 1948. In the radio region the spectrum is like a power law, with index » 0.3, and the source is also polarised (at 3 cm wavelength by about 7%) with a similar amount detected in the optical. All of these are strong evidence for synchrotron emission.
The Crab is thought to be the result of a so-called Type I Supernova. It is about 2 kpc distant and has an angular size of about 4 arc-minutes.

Images of the Crab in X-ray, optical, IR and radio can be seen in Fig 4.6, with further details provided at http://chandra.harvard.edu/photo/0052/what.html.
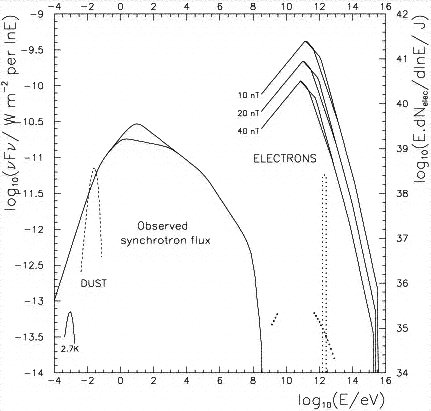
A spectrum is shown in Fig 4.7, showing the synchrontron spectrum with a turnover at about 100 keV. There is possibly a inverse-Comptonised spectrum at very high energies (1010-1012) eV. More about Compton scattering later in the course.
The total luminosity of the Crab is L » 5 ×1038 erg sec-1.
Consider electrons in the Crab Nebula synchrotron radiating at 20 keV (n.b. 1eV = 1.602 ×10-12 erg) or n = 4.8 ×1018 Hz, for a magnetic field strength of order 10-4 Gauss. For these electrons the Lorentz factor is
| (27) |
the electron energy is
| (28) |
and the emitted power is
| (29) |
The cooling time is of order
| (30) |
which is much shorter than the age of the nebula. This indicates that there must be a fresh supply of high energy electrons into the nebula: the pulsar is the usual culprit implicated in this matter, since its spin-down energy loss is very close to the synchrotron energy output.
The synchrotron spectrum turns over (figure 4.7) at about 1016 Hz (or 40 eV). The cooling time at this frequency is about 1300 years, which is of the same order as the age of the nebula.
The pulsar (or neutron star) in the Crab Nebula rotates with a frequency of w = 190 sec-1, and is slowing down at a rate [(dw)/dt] = -2.4 ×10-9 sec-2.
|
Problem 4.5 Consider the pulsar to be a solid body of uniform density with mass M and radius R, for which the moment of inertia, I = [ 2/5]MR2 and the rotational energy is E=[ 1/2]Iw2. a) show that the pulsar is losing energy at a rate given by
b) If the mass of the pulsar is M » 1 MO and the radius is R » 10 km, show that energy is being lost by the pulsar at a rate which is very close to the observed luminosity of the surrounding nebula.
|
The nebula emits X-rays at 105 eV, which can be associated with the peak of the synchrotron spectrum at 0.29nc. The magnetic field in the nebula has a strength of B » 10-4 Gauss.
|
Problem 4.6 Show that the electrons which produce these X-rays have
Hence compute the energy of the electrons producing this radiation, and the synchrotron power radiated per electron if they are isotropic. How long can the electrons radiate X-rays at this rate? Show that this is much shorter than the known age of the Crab.
|
The previous problem shows that the electrons in the Crab can radiate away their KE in a time much shorter than the age of the Crab itself. One might conclude from this that there is a continuous source of fresh, high energy electrons being injected into the nebula from the central pulsar.
|
Problem 4.7 The synchrotron spectrum of the Crab shows a change of slope at around 1015 Hz, thought to be due to the high energy electrons, which are able to radiate their energy away in a time shorter than the age of the nebula. Show that at this frequency the electrons have a lifetime which is about the same as the age of the Nebula, if the magnetic field strength is B = 10-4 Gauss.
|
|
Problem 4.8 One mechanism for the pulsar to lose energy is magnetic dipole radiation. If the spin axis of the pulsar is at an angle q to the magnetic axis, then the rotating magnetic field radiates energy at a rate
where m is the magnetic dipole moment. By equating P with -dE/dt above, show that
and hence that
where C is a constant and wi is the initial rotation rate of the pulsar. Using the current rotation rate w and the current slowdown rate [(dw)/dt] to show that C = 3.49×10-16 sec. (w = 190 sec-1, and [(dw)/dt] = -2.4 ×10-9 sec-2). Show that these values imply that the age of the nebula is not more than 1254 years, in good agreement with the known age.
|