Matter falling onto some body is termed accretion. Suppose the matter is falling onto a star of mass M and radius R. Falling freely, it gains kinetic energy in exchange for potential energy. For a mass m falling from infinity to a distance r from the central mass, the KE matches the PE as
| (1) |
The mass eventually hits the surface of the star and its KE is released as heat, and appears in some form of radiation. For an accretion rate dm/dt, the KE is turned into heat at a rate [ 1/2][ dm/dt]v2ff, or the luminosity L is
| (2) |
|
Problem 6.1 The Schwarzschild radius of a black hole is given by
Show one can write the down the accretion luminosity as
|
The result of this is that the luminosity can be expressed as
| (5) |
In this form x can be seen to be the efficiency of the conversion of rest mass energy into luminosity!
|
Problem 6.2 Show that the efficiency x for a solar mass white dwarf star, for which the radius is of order 5 ×108 cm, is x » 3 ×10-4. What is the efficiency for a solar mass neutron star, with radius of order 10 km? How do your answers compare with the efficiency for the release of energy via the p-p chain, for which x » 10-2?
|
The problem above shows that more energy is released for a more compact object. The most ``compact'' object one can imagine is a black hole, but the problem here is that there is no surface for the matter to fall onto. As a general problem in any case, in-falling matter will always possess a certain amount of angular momentum, and this will prevent it falling directly onto the compact object. The matter may instead be able to form a coherant and steady structure called an accretion disk, which is a more or less thin disk of material in quasi rotational equilibrium around the central mass. Viscous forces acting in the material in the disk allow angular momentum to be transfered outward and the matter which has lost angular momentum to fall further into the gravitational well.
For black holes, various relativistic effects must be taken account of, and this results in efficiencies ranging from x » 0.1 to » 0.4, depending on the rotation of the black hole (fast rotating black holes being more efficient).
This is a remarkable efficiency, and black holes are thus excellent candidates for the large energies which are emerging from such objects are X-ray binaries and quasars.
Eqn 6.4 shows that, for a constant accretion rate dm/dt, the radial dependence of the luminosity of the disk L(R) is
| (6) |
If this luminosity is produced as blackbody radiation, then
| (7) |
so that the temperature profile, T(R), of the disk is
| (8) |
More generally, one may put
| (9) |
Real accretion disks are found to have a fairly large range of exponents a, ranging between 0 to 1, rather than clustering around 0.75 (for example, the model for GRO-J1655-40 by Orosz and Baylin had a » 0.2). Accretion is found in a wide range of astrophysical objects: stellar mass black holes (X-ray binaries), young stars/pre-main sequence stars, active galactic nuclei/quasars, proto-planetary disks and so on. Before looking at a few cases though, we'll address a couple of related issues.
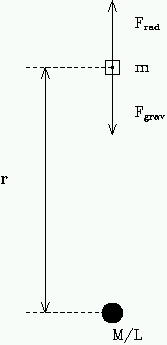
Consider a small cloud of ionised matter of mass m near a luminous object, such as a hot star, with a mass to luminosity ratio of (M/L) (see figure 6.1). It can be shown that the radiation force outward on the cloud is
| (10) |
where L is the luminosity of the central source and k is called the mass absorption coefficient of the cloud, (i.e. the cross-section per unit mass).

|
Problem 6.3 What is the force on the cloud due to the gravity of the central mass? From outward and inward forces on the cloud show that if
then the cloud will be forced away by radiation pressure.
|
|
Problem 6.4 A minimum value for k is that due to Thomson scattering off free electrons, where we consider the cloud to be fully ionised Hydrogen. Show the maximum luminosity that a central mass M can have while not ejecting matter spontaneously is
where mH is the mass of the Hydrogen atom. Hence, show that
|
|
Problem 6.5 Using the mass and luminosity of the Sun, how close is the Sun to the Eddington limit? A 60 solar mass star is quite close to the Eddington limit. How much more luminous is such a star than the Sun? In what spectral region would the energy distribution of such a star be expected?
|
There are a number of X-ray sources in the Galaxy and in the Large Magellanic Cloud (LMC), which have X-ray luminosities quite close to the Eddington limit for a solar mass central object, » 1031 W or 1038 erg s-1.
The flux from a object cannot vary faster than the light travel time across the object, unless special conditions apply such as relativistic beaming. X-ray binaries, such as GRO J1655-40, show rapid variability, on the time scale of milliseconds. Rapid variations of this type are called ``flickering''. The light travel time across the region occupied by solar mass black hole is of order 10-5 sec, which is well consistent with the flickering observed. Super-massive black holes, for which excellent evidence exists from studies of the central regions of nearby galaxies with the Hubble Space Telescope, and which are thought to reside at the centers of quasars, also show flickering on much longer time scales (hours to days) which is consistent with their larger masses. From the light travel time to cross the Schwarzschild radius, one can show that the minimum time scale for flickering is given by
| (14) |
Assuming that the luminosity of black holes is generated at the Schwarzschild radius, one can derive a temperature for the emitted radiation as a function of mass,
| (15) |
|
Problem 6.6 Prove the result above.
|
|
Problem 6.7 A typical quasar has an X-ray luminosity of 1037 W and a inferred central black hole mass of 108 MO. Show that this is well below the Eddington luminosity. What temperature would one associate with the radiation if it were black body?
|
The problem above shows that quasars and AGN (Active Galactic Nuclei) might have some kind of emission in the UV. This is indeed the case, with many exhibiting extra UV radiation which is called the ``blue bump''. This may well be associated with the inner regions of the accretion disk.
Disks may be thin or thick. Thin disks are essentially 2-dimensional and their physics is considerably simplified by this convenient property. If the internal pressure forces in the disk become large enough to act against the vertical gravitational field, the disk is free to expand and its physics must be described in full 3-D.
Quite simple arguments can be made in the case of thin disks in deriving their temperature profile and expected radiation, assuming that the surface radiates like a black body at the local temperature. More detailed physics shows that the inner regions can be optically thin, so that black body radiation is no longer a good assumption. In this case, the result is bremsstrahlung radiation from the ionised inner disk.
|
Problem 6.8 Assume that the accretion rate is fixed, and the disk radiates like a blackbody, and has an inner boundary at r1 and an outer edge at r2. From Eqn 6.8, and the blackbody emission law
show that, over a certain frequency range
Which regions of the disk are responsible for the various marked parts of the total spectrum shown in figure 6.2?
|
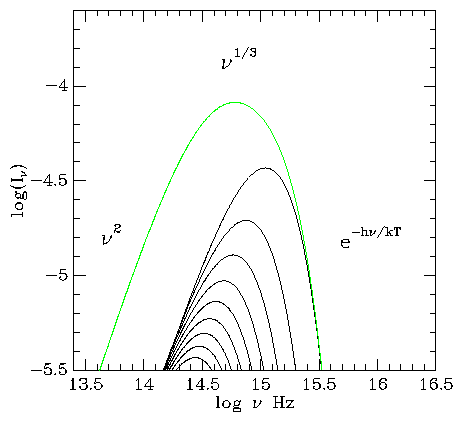
Thick disks are very much more complicated to treat than thin disks, and it is not yet clear if a consistent solution has been found. One feature of thick disks is that they may help explain the jets which emerge from many sources of this type, although this is again far from proven.
Pre-main-sequence objects are stars which are in the final stages of formation - the star itself has formed, but can still heavily obscured by the dust and gas from the cloud from which it formed. In the case study here, HD 34282, the star has a proto-planetary disk.
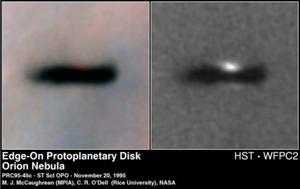
HD 34282 is a A0V-A3V star with a rotational velocity (vsin i) of about 130 km/s - very fast for a star, and quite usual in very young stars. It varies between about 9.8 and 10.1 apparent V magnitude, and has a parallax (Hipparcos) of 6.10 ±1.63 mas, coresponding to a distance of 160 pc (1-sigma bounds of 130 to 220 pc). With this parallax, its luminosity is about 5 LO. There is a significant flux excess in the IR, as shown in figure 6.4. Modelling these systems is quite a challange, especially in the case of HD 34282, for which several components are required to model the IR excess. Careful analysis of the primary star's position in the colour-magnitude diagram indicates that it is only a few Myr old.
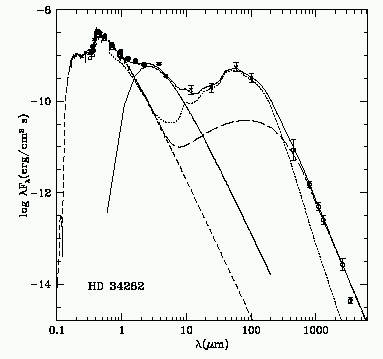
The disks of these systems ought to be in Keplerian rotation, and recent observations have detected this, at least for the outer parts of the disks.
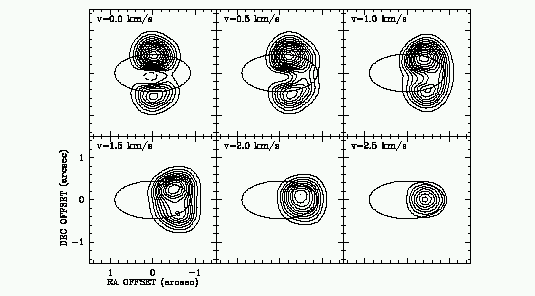
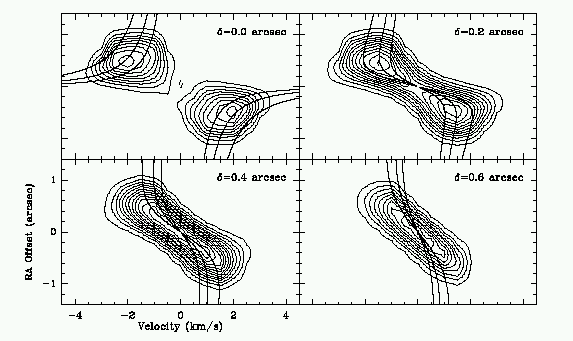
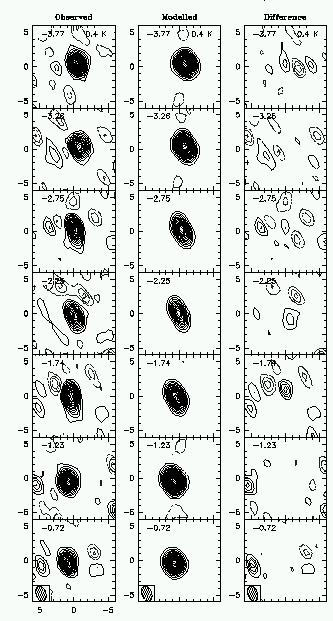
Accretion need not take place through a disk. Under the right circumstances, material can flow directly onto a compact object. This can happen for example when a giant star, which has a strong outflow of material (called a stellar wind) is in obit around a massive compact object. Some of the material passes by the compact object and flows directly onto it.
Another case is accretion onto white dwarfs, which leads to novae and a certain kind of supernova called Type I. Novae are of course ``new stars'' which rise rapidly to great brightness (up to 10 magnitudes or 104 times) over a few days and then slowly fade over a few months. It is thought that a companion star is providing the accretion material which settles onto the white dwarf in a column or stream, is compressed and heated to very high temperatures, more than 107 K. This is hot enough for nuclear burning to take place, and can lead to runaway burning if the amount of accreted material is sufficient. The temperatures get high enough that considerable CNO burning can take place, and this appears to be the explanation for the large amounts of these elements which are eventually ejected by the star. Much of the accreted material is eventually ejected from the white dwarf surface after being rapidly processed at these high temperatures. Nova radiate close to the Eddington limit for a short time.
Type I supernovae involve yet more dramatic events. Accreting matter onto the surface of a white dwarf takes it over the mass limit below which it is able to maintain itself from gravitational collapse through internal pressure (due to degenerate matter). This is known as the Chandrasekhar limit, and is about 1.4 MO. The process then leads to further burning in the core of the star, which has not taken place since the giant branch phase earlier in its life. The resulting supernova explosion is thought to totally disrupt the star, with most of the energy going into the outward expanding plasma, a supernova remnant. The light curves of type I supernovae are very similiar, as expected for a white dwarf just exceeding the Chandrasekhar limit.
This section is based on an article by A. C. Fabian (1997) in Astronomy and Geophysics vol 38, issue 4, page 10.
The central regions of accretion disks around neutron stars or black holes probe the strongest gravitationl fields we know about. Practically all the kinematic evidence we have for black holes does not probe very close to the black hole, in fact, the best evidence at the moment is rarely closer to the black hole than about 100,000 gravitational radii (or Schwarzschild radii). The way to get closer is to probe the inner edge of accretion disks. The problem here is that the gas is very hot and ionised, and it is difficult to measure how fast it is moving around the black hole when the emission is mostly due to continuum mechanisms. At temperatures typical of X-ray emission there are some very interesting lines, due to FeXXV and FeXXVI.
There is a thin ionised atmosphere above the accretion disk, which emits X-rays, some of which travel back toward the disk, are reflected and stimulate emission of Fe lines from the atmosphere, such as the 6.4 keV line. These lines, if they can be detected by an X-ray telescope of sufficient spatial and spectral resolution, would allow us to map the motions of the material flowing around the black hole very close to the Schwarzschild radius.
Simulations have shown that the shape of this line is very sensitive to the viewing angle we have of the disk, and also to the amount of spin of the black hole. There are other effects, such as the time dilation caused by observing the receeding and approaching sides of the accretion disk, and the gravitational redshift caused by the potential well of the black hole. The result can be a two-peaked line profile (for a Schwarzschild/non-rotating black hole) or a skewed, flat topped profile (Kerr black hole) either of which can tell a great deal about the black hole and inner accretion disk.
Attempts were made to observe this effect were made with the Japanese X-ray satellite, GINGA, but it was unable to resolve the line clearly. ASCA (Japan-USA) observed the line for the first time and demonstrated that the velocities involved were of order 50,000 km s-1, as expected for material close to a massive black hole. Further observations led to the line being resolved, and first parameters for the accretion disk being derived. The best fit was for a disk inclined at about 30 degrees to the line-of-sight and for a rapidly spinning (Kerr) black hole. This is a remarkable confirmation of the basic ideas about these sources.
X-ray missions such as XMM (Newton) and AXAF (Chandra) offer greatly increased sensitivity and should be able to map the inner regions of accretion disks around black holes in detail. First indications (in 2003) for Kerr type black holes are now available, as a result of very long (21 hours) exposures with XMM/Newton.
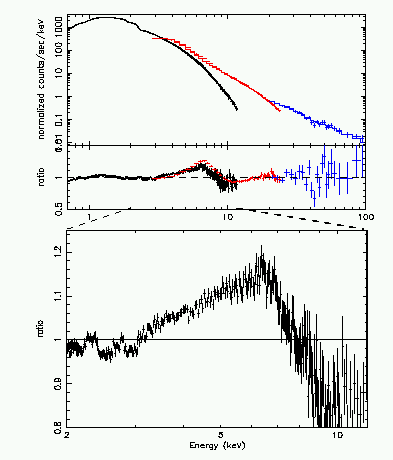
GX 339-4 is a Galactic black hole candidate, with a central black hole mass of at least 6 MO, with near relativistic radio jets and a low mass (K dwarf?) companion.
For a rapidly spinning black hole the inner edge of the accretion disk can be considerably closer to the event horizon than for a non-rotating BH. For a maximally spinning BH, the inner edge can be as close as 1.2 rg, where rg=GM/c2 is the Schwarzschild radius. This is about 5 times closer than for a non-rotating black hole, and the velocities of the material can be very much higher, but there is also the very interesting effect that there is a gravitational redshift from the BH. Fitting of the spectrum shown by Miller et al 2003 (Fig 6.8) indicates that the inner edge of the disk is at 2-3 rg, indicating the BH is spinning quite rapidly. Fits with standard Schwarzschild BH result in poor fits, and can be ruled out with high significance (8-s).
|
Problem 6.9 Find out the relativistic formulae for doppler shift and gravitational redshift. Assuming that the Fe line in Figure 6.8 originate from 2-3 Schwarzschild radii, estimate the size of the redshifts and blueshifts involved. Are you answers consistent with the figure?
|
Further Resources
HST image of outer regions of disk material in NGC 4261
3-D simulations by Michael Owen
Chandra Pinpoints Edge Of Accretion Disk Around Black Hole
Global simulations of accreting black holes
Protoplanetary Disks in the Orion Nebula