Lecture 7 : Compton Scattering

1  Introduction

Thomson scattering, or the scattering of a photon by an electron at rest, strictly only applies at low photon energy, i.e. when hn << m_e c².

If the photon energy is comparable to or greater than the electron energy, non-classical effects must be taken into account, and the process is called Compton scattering. A further interesting situation develops when the electron is moving - in this case energy can be transferred to the photon, and the process is called inverse Compton scattering. This last process is an important mechanism in high energy astrophysics.

2  Thomson scattering

In Thomson scattering, we have

dsT dW =  1 2 r02 (1 + cos2q)

(1)

where s_T is the Thomson cross-section, W the solid angle, q is the angle of scattering, and r₀ is the classical electron radius,

r0 =  e2 me c2 .

(2)

In Thomson scattering the incident photon and scatter photon have the same wavelength or energy, so this scattering is also called coherent or elastic.

If we now move to photons of energy hn\ga m_e c², the scattering is modified by the appearence of quantum effects, through a change in the kinematics of the collision, and an alteration of the cross-section.

3  Compton Scattering

To do the kinematics of the collision correctly at high photon energy, momentum and energy must be conserved.

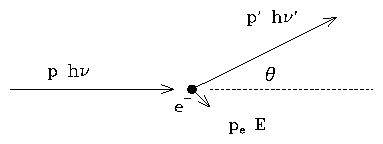
Let the incident photon have energy hn and momentum hn/c, the scattered photon have energy hn¢ and momentum hn¢/c, and the electron (initially at rest) acquires energy E and momentum p_e. The scattering angle is q.

Figure 1: Compton scattering of an incident photon of energy hn and momentum p to energy hn¢ and momentum p¢. The electron is initially at rest and acquires energy E and momentum p_e.

In terms of wavelength, this reduces to

l¢- l = lC (1 - cos q)

(4)

where l is the incident photon wavelength, l¢ is the scattered photon wavelength and l_C is the Compton wavelength and is given by

lC =  h me c = 0.02426  Å.

(5)

The compton wavelength can be regarded as a wavelength change Dl in the incident photon. Note that for l >> l_C the change is negligible and we get back the Thomson scattering.

In full treatment of the problem yields the Klein-Nishina formula for the scattering cross-section:

ds dW =  r02 2 æ è  n¢ n ö ø 2   æ è  n n¢ +  n¢ n - sin2 q ö ø

(6)

which can be shown to yield the following formulae for the total cross-section (where x = [(hn)/(mc²)]),

s » sT æ è 1 - 2x +  26x2 5 + ... ö ø ,   for   x << 1,

(7)

and

s =  3 8 sT  1 x æ è ln(2x) +  1 2 ö ø ,    for   x >> 1

(8)

for the non-relativistic and extremely relativistic cases. The main effect is thus to reduce the cross-section at high photon energies, i.e. the scattering of the photons becomes less efficient.

4  Inverse Compton: scattering from moving electrons

An important case arises when the electrons are no longer considered to be at rest. In inverse scattering, energy is transferred from the electrons to the photons, i.e. it is the opposite of Compton scattering, in which the photons transfer energy to the electrons. Inverse Compton scattering can produce substantial fluxes of photons in the optical to X-ray region. Analysis shows that the mean frequency of the photons after the collision increases by a factor g², so that high frequency radio photons in collisions with relativistic electrons for which g is of order 10³ to 10⁴ can be boosted in the UV and X-ray regions. There is a practical limit to the amount of boosting possible beyond the Thomson limit (hn » gmc²), which can be seen from the conservation of energy

hn¢ = gmc2 + hn.

(9)

Scattered photon energies are thus limited to gmc².

The power emitted in the case of an isotropic distribution of photons is

PComp =  4 3 sc Urad g2 b2

(10)

where U_rad is the radiation energy density of the photon field (before scattering).

Note how similiar this is the power due to synchrotron emission

PSynch =  4 3 sc UB g2 b2

(11)

where U_B is the energy density of the magnetic field. Thus

PSynch PComp =  UB Urad .

(12)

The losses due to synchrotron and Compton processes are in the ratio of the magnetic field energy density to the photon field energy density, and is independent of g.

The scattered photons may be produced in the source through synchrotron radiation, and if these are bossted then the resultant photons are called Synchrotron Self Compton.

5  Comptonisation

If the spectrum of a source is primarily determined by Compton processes it is termed Comptonised. In this case the plasma must be thin enough that other processes, such as bremsstrahlung, do not dominate the spectrum instead. The hotter the gas, the more chance of Comptonisation.

Some examples of astrophysical sources in which comptonisation is important are:

• hot gas near binary X-ray sources

• hot plasma in clusters of galaxies

• hot plasma near center of active galactic nuclei

• primordial gas cooling after the Big Bang

5.1  Non-relativistic Comptonisation

We consider non-relativistic electrons and photons with energy hn << m_ec². From Eqn 7.4 one can show that the relative change in the photon energy DE/E is given by

DE E =  hn mec2 (1-cosq)

(13)

In the electron frame, the scattering is Thomson, and therefore symmetric around the incident direction, so that

DE E =  hn mec2 ,     for hn << mec2.

(14)

This is the average energy increase of the electron for low photon input energies, hn << m_e c².

Now consider high energy photons. In this case the power produced per scattering is given by Eqn. 7.10. For non-relativistic electrons, g » 1, so for electron velocity v,

PComp =  4 3 sc æ è  v c ö ø 2   .

(15)

The number of scattered photons per second is the number of photons encountered per second by an electron, which is given by the photon number density, N_phot, the photon velocity c and the Thomson cross-section s_T

Nphot c sT.

(16)

The photon number density is just

Nphot =  Urad hn

(17)

so we have

sT Nphot c =  sT Urad c h n .

(18)

Comparison of Eqns. 7.15 and 7.18 readily shows that the energy gain of the photons per collision must be

DE E =  4 3 æ è  v c ö ø 2       for hn >> mec2.

(19)

Let's summarise what we have so far:

• For h n << m_e c², the electrons gain energy. (Eqn 7.14).

• For h n >> m_e c², the photons gain energy. (Eqn 7.19).

5.2  Thermal electrons

To make things practical, let's consider a thermal distribution of electrons, with temperature T_e. We have

3 2 k Te =  1 2 me v2

(20)

where v is the typical electron velocity. Eqn 7.19 can thus be written

DE E =  4kTe mec2     for hn << kTe.

(21)

If we now combine the results of Eqns 7.21 and 7.14 we can derive a simple equation for the energy gain/loss for both the high and low frequency regimes

DE E =  1 mec2 (4kTe - hn).

(22)

Therefore, for

• hn = 4kT_e, there is no energy exchange

• hn > 4kT_e, electrons gain energy

• hn < 4kT_e, photons gain energy

The usual case of interest is hn < 4kT_e, i.e. the electrons are ``hotter'' than the photons.

6  The Compton parameter

Now consider a plasma cloud of electron density n_e and characteristic size D. The optical depth t_e to Compton scattering is just

te = ne sT D.

(23)

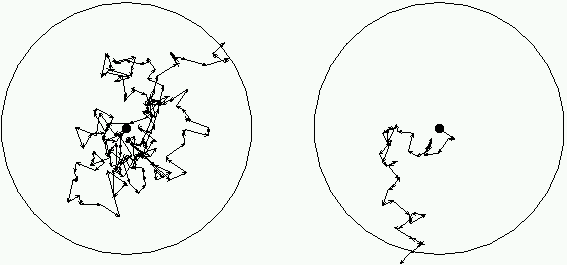
If t_e >> 1, the cloud is optically thick, and a large number of scatterings are required for a photon to escape from the cloud. The path taken by the photon to get out of the cloud is termed a random walk. Figure 7.2 illustrates two possible paths for a photon executing a random walk from the center of an optically thick region until it reaches the edge and escapes.

Suppose the photon typically moves a distance l before being scattered. In order to escape from the cloud, the photon must move a distance D where

D = ÖN l

(24)

where N is the number of scatterings.

The mean free path l is given by

l =  1 ne sT .

(28)

After one scattering, the initial energy E is increased by DE, where

DE E = 1 +  4kTe me c2

(29)

and so after N scatterings, the energy is E¢ where

E¢ E = æ è 1 +  4kTe me c2 ö ø N   .

(30)

We now define y, the called the Compton y-parameter, as

y = (Number of scatterings) ×(Energy gain/scattering).

Figure 2: Compton scattering of a photon in a mildly optically thick region. The photon begins at the central dot and executes a random walk until it reaches the edge of the cloud and escapes. A shorter and a longer random walk are shown.

6.1  Weak Comptonisation

6.2  Strong Comptonisation

In strong Comptonisation, the photon energy is increased until the electron and photon energy distributions approach equilibrium, i.e. there is further no net energy gain by one population to the other. In this case the photons are ``heated'' to such a temperature that

hn = 4 k Te.

(32)

Let the optical thickness necessary for this to happen be t. If the medium is optically thick, then a large number of scatterings are required for photons to escape. The number of scatterings N is given by Eqn 7.27, and it thus follows from Eqn 7.31 that

4kTe hn0 = exp é ë 4  kTe me c2 t2 ù û .

(33)

In this case the medium will be strongly Comptonised, and the photon spectrum will approach an equilibrium form given by

un =  8 ph n3 c3 é ë exp æ è  hn kT +m ö ø ù û -1   .

(34)

This form, for m = 0, is just the Planck (or blackbody) spectrum. When the equilibrium state involves two species (photons and electrons), then we can introduce a chemical potential between them, m. The effect on the Planck spectrum is illustrated in figure 7.3 for various potentials m.

Figure 3: Comptonisation of photons for various values of the potential, m. From top to bottom the curves show the spectrum for m = 0, 0.1,0.3. 1.0, 3.0 and 10.0. Note that m = 0 is the pure black-body curve.

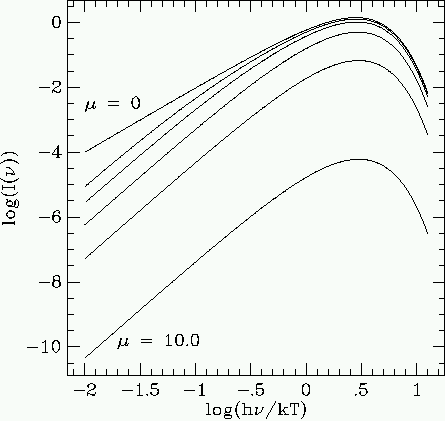
For m >> 1, the spectrum at high frequency approaches the Wien spectrum with an extra factor of e^-m,

un =  8 ph n3 c3 e-m e-[(hn)/kT]

(35)

and at low frequency

un µ n3.

(36)

Figure 4: Saturated Comptonisation of a bremsstrahlung spectrum. See text for details.

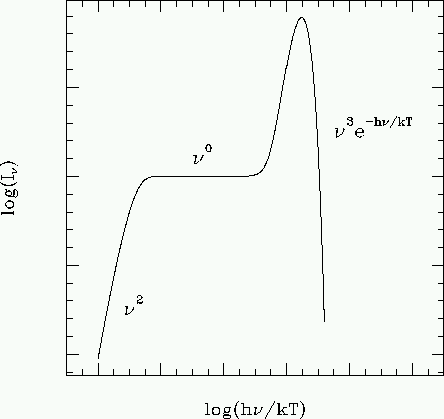
Figure 7.4 illustrates strong comptonisation of a bremsstrahlung spectrum in an optically thick, non-relativistic medium. The bremsstrahlung spectrum dominates at low frequency and shows a characteristic self-absorption region (I_n µ n²) and a flat region (I_n µ n⁰). At higher frequency, photons have been multiply scattered via the Compton process so that a Wien spectrum forms (I_n µ n³ e^-hn/kT).

7  Kompaneets Equation

In the previous section we derived forms for the spectrum when the amount of Comptonisation in a non-relativistic medium is weak and strong. What about intermediate cases? The equation which describes these cases was derived by Kompaneets in 1949. Its derivation is non-trivial. The equation involves the evolution of the distribution of the photons in phase space, n,

¶n ¶y =  1 x2  ¶ ¶x é ë x4 æ è n + n2 +  ¶n ¶x ö ø ù û

(37)

where

x =  hn kT

(38)

and the compton y-parameter is generalised to an integral along the photon path

y = ó õ  kTe mec2 sT ne dl

(39)

and where the terms in the square brackets represent

• the increase/decrease in photon numbers in frequency space, (the [(¶n)/(¶x)] term)

• cooling of photons/electron recoil, (the n term)

• and the cooling due to induced Compton scattering, (the n² term)

In general, solutions to the Kompaneets equation must be found numerically, although there are some useful limiting cases which can be solved analytically.