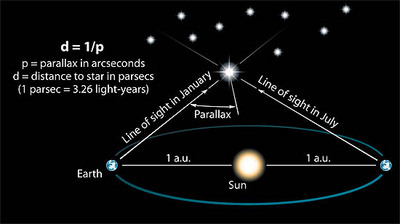

Until the late 1980's only a few hundred stars had been measured accurately in this way, since the effect is very small and difficult to measure with ground based telescopes. The European Space Agency's Hipparcos mission revolutionised this field, measuring the parallaxes of some 120,000 stars, some 15,000 with an accuracy of better than 10%. Distances, D (in parsecs, pc), allow the absolute magnitude MV of the stars to be determined using the apparent magnitude V.
MV = V - 5 log (D) + 5
The apparent magnitude is a measure of the flux from the star as seen at the Earth in a particular pass-band (or filter). The simplest such system for optical light measures the flux in five filters termed U, B, V, R, I for ultra-violet, blue, visual, red and infra-red. The colour index of a star is defined by the logarithmic ratio of the flux in two filters
B - V = 2.5 log(Flux in B/Flux in V)
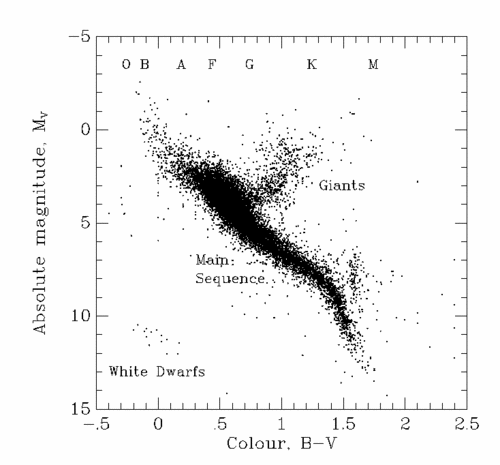
This leads to the Colour-Magnitude Diagram (or CMD) in which the colour of stars is plotted against their absolute magnitudes. The CMD of the Hipparcos stars for which the distances were measured to better than 15 % is shown below:
| Exercise #1: A list of nearest
stars to the Earth can be found at this
link.
Select appropriate data from the table, and plot the stars on the CMD above. You will see that "spectral types" have been indicated for the stars, using a system of subtypes --- which splits the OBAFGKM system into a more precise system. The subtypes run from 0 to 9 within each spectral class -- G0 to G9, or M0 to M9 are examples. Following the spectral type is an addition "luminosity class", which for most stars in the table is "V" -- indicating a dwarf or "main sequence star." The other types available are I, II -- supergiants (very luminous stars), III -- giants (luminous) IV -- subgiants (intermediate luminosity between giants and the main sequence) and finally V for the main sequence (dwarfs). What does the spectral type "D" mean? Make an estimate of the stellar density in the solar neighbourhood (in stars per cubic parsec) from your data. For additional data on each star (such as its colour index, B-V) you can search the huge database Simbad. You can also get the parallaxes of the stars from here, and confirm the absolute magnitudes in the table. |
The spectral types are (very roughly) indicated at the top of the
diagram. The broad sweep of stars from upper-left to lower-right is
called the main sequence, and is the site of Hydrogen burning. After
stars on the main sequence exhaust their fuel they move off the main sequence
and become giants (most of the giants seen in the diagram would have
been A-G main sequence stars up until a few million years ago), later ending up
in the stellar graveyard as white dwarfs.
The following table shows the amount of gas and stars of various types in
the solar neighbourhood. The total amount of non-stellar material, integrated
over 1 square parsec above and below the Sun's position is about 13
Mo. The total amount of stellar material is about 35
Mo, giving a total of 48 Mo per square parsec. The total
mass density of matter near the Sun is about 0.1 M0 per cubic
parsec.
| Component | volume density | vertical velocity dispersion |
surface density | |
| Mo pc-3 | km s-1 | Mo pc-2 | ||
| Gas | Molecular Hydrogen H 2 | 0.021 | 4.0 | 3.0 |
| Ionised Hydrogen H I | 0.028 | 8.0 | 8.0 | |
| warm gas | 0.001 | 40.0 | 2.0 | |
| Stars | giants | 0.0006 | 17.0 | 0.4 |
| MV < 2.5 | 0.0031 | 7.5 | 0.9 | |
| 2.5 < MV < 3.0 | 0.0015 | 10.5 | 0.6 | |
| 3.0 < MV < 4.0 | 0.0020 | 14.0 | 1.1 | |
| 4.0 < MV < 5.0 | 0.0024 | 19.5 | 2.0 | |
| 5.0 < MV < 8.0 | 0.0074 | 20.0 | 6.5 | |
| MV > 8.0 | 0.014 | 20.0 | 12.3 | |
| white dwarfs | 0.005 | 20.0 | 4.4 | |
| brown dwarfs | 0.008 | 20.0 | 6.2 | |
| stellar halo | 0.0001 | 100.0 | 0.6 |
Some nice round numbers to remember :
Young, metal rich stars rotating with the disk of the Galaxy are termed
Population I, while old, metal weak stars are termed Population
II. The fundamental difference between these two types relates to when and
how they were formed.
The very youngest stars are of type O and B, and are found in associations and clusters, often still containing the protostellar gas (gas from which stars will form). Hot stars of this type light up the gas clouds around them by ultra-violet photo-ionisation, causing the clouds to glow conspicously in the light of Hydrogen emission lines --- these are called HII regions. Cold gas clouds, which are in the process of collapsing under gravity before stars begin to form, can be detected via emission from molecules such as CO.
All of these objects, as well as much of the gas layer, are concentrated very close to the galactic plane, with a scale height of about 100 pc. Scale height hzis defined as the exponential falloff in density (ρ) of the stars or gas as a function of height z above the Galactic plane: ρ(z) = ρ(0) e(-|z|/hz)
|
On metallicity or abundances of stars The amount of heavy elements or metals in stars relative to the amount in the Sun is called the metallicity or the abundance and is denoted by the symbol [X/H] (note the square brackets). [X/H] = log(X/H)star - log(X/H)Sun where X is an element (or group pf elements). Note that this defines the solar metallicity as [X/H] = 0.0. Fe (iron) is a commonly measured element in stars. A star with a metallicity of [Fe/H] = -1.0 has 10 times less metals than the Sun relative to Hydrogen, while a star with twice the metallicity of the Sun has [Fe/H] = 0.3. |
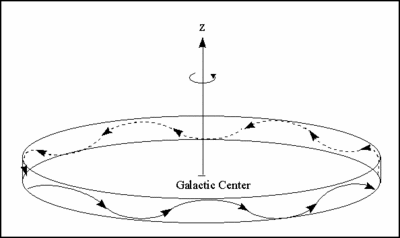
Motions of Stars in the disk. Source:
http://astrosun.tn.cornell.edu/courses/astro201/circ_motions.htm
|
The space velocity of a star can be determined by measuring its distance, proper motions and radial velocity. The space velocity is a star's true motion in space relative to some system, such as the Cartesian Galactic system of coordinates (defined above). The radial velocity is the component of the space velocity projected along the line of sight from us to the star. The proper motions are the angular movement of the star projected onto the sky as seen from the Earth. Radial velocities are measured using the spectral redshift, in which the spectrum of the star is shifted to the blue if it is moving towards us or the red if moving away. The proper motions are measured by observing the star's very small motion across the sky relative to other stars, usually by measuring its exact position over many years.The radial velocity of a star is in general much easier to measure than the proper motions. The three components of a star's velocity along the Galactic coordinate system (X, Y, Z) are usually termed (U, V, W), and are defined by the following time derivatives: U = dX/dt
In physical terms, U is the velocity of the star toward the Galactic center, V is its velocity in the direction of Galactic rotation, and W is its velocity out of the Galactic plane. The velocity dispersion of a group of stars is usually measured by the RMS (root-mean-square) scatter in the velocities. These are denoted by σ in each of the three components: (&sigmaU,&sigmaV,&sigmaW) where (for example) the velocity dispersion in V is
In physical terms, the velocity dispersion is a measure of the kinetic energy of the group of stars, and is closely related to how the stars will move within the Galactic gravitational field. |
The velocity dispersion of stars of the young disk is the smallest of all the stellar populations -- typically amounting to 10-20 km/s.
The old disk refers to objects on the disk with ages of more than a few Gyr. This broadly means F-type stars or "later" (for historical reasons hot, blue stars are called early type while cool, red stars are called late type).
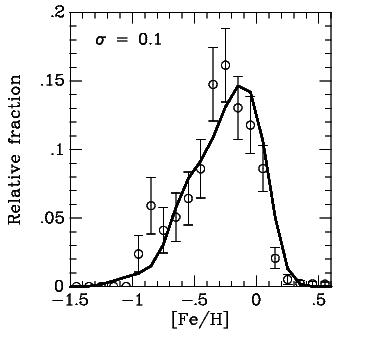
The old disk rotates at about 200 km/s rather than 220 km/s (as the young disk and gas do) so that it lags behind the young disk. The total velocity dispersion is about three times that of the young disk, 40-60 km/s. Objects of the old disk include, F, G, K and M stars, white dwarfs, planetary nebulae and some types of variable star. Perhaps 80% or 90% of the local material belongs to the old disk. The abundances of old disk stars range from about [Fe/H] = -0.5 to [Fe/H] = 0.3. Most of the stars have abundances in a narrow peak at a value a bit less than the Sun, [Fe/H] = -0.2, as seen in the next figure, and there is a weak tail extending to [Fe/H] = -1.0.
The old disk has a scale height of about 250 pc, 2 to 3 times greater than
the scale height of the young disk. We'll see in a later lecture that this is
thought to have arisen due to processes in the disk of the galaxy which "heat"
(increase the velocity dispersion, at the expense of systemtic rotation around
the galaxy) of stellar orbits over long time scales (of order Gyrs).
The bulge luminosity distribution can be modelled by a de Vaucouleurs' law with Galactocentric radius R
I(R) = Ie exp(-7.67 ( (R/Re) )-1)
where Re is the projected half light radius and Ie is the surface brightness at Re.
The density distribution, ρ, of the stellar halo follows a power-law with Galactocentric radius, R
ρ(R) = R-&alpha
where α has been measured directly from halo stars to have a value of α = 3.5 +/- 0.5.
Both the bulge and halo are centrally concentrated --- that is most of their mass and light is within the solar circle (the orbit of the Sun around the center of the Galaxy at R = 8 kpc).
Typical stellar halo objects are globular clusters, subdwarf stars, certain kinds of RR Lyrae stars and long period variables. Subdwarfs are low mass (< 1.5 M0) metal weak, stars which typically lie 1 to 2 magnitudes below the main sequence (as defined by metal rich disk stars --- see above).
The stellar halo is old, with ages for typical objects known to lie in the range 12-14 Gyr. This has been determined from the colour magnitude diagrams of globular clusters and nearby subdwarfs. It would seem that the halo stars were the very first to form as the Galaxy was collapsing from a gas cloud in the early universe. As a consequence they retain information about this early time.
Neither the halo or bulge rotate very much. The halo rotates very little,
with a systemic velcoty around the Galactic center of about 20 +/- 20 km/s,
(compare to the disk rotation of 220 km/s). This means that the halo is
pressure supported, unlike the disk which is rotation supported.
Halo stars have a large velocity dispersion (in all three components) of about
120 km/s and this is what keeps them in their spheroidal configuration. The
bulge rotates slowly at about 100 km/s and has a velocity dispersion of about
100 km/s. Hence it is somewhat intermediate between the disk and the halo in
these respects.

Random motions : The stars in star clusters and in the spheroidal components of galaxies, and the galaxies in clusters of galaxies, have motions that are random in three dimensions. That is, they have no preferred plane (disk).
Source:
http://astrosun.tn.cornell.edu/courses/astro201/random_motions.htm
| Population I | Population II | |
| Age | Young disk : < ~1 Gyr
Old disk : ~1 - 10 x 109years |
12-15 x 109 years |
| Metallicity [Fe/H] | −0.5 <~ [Fe/H] <~0.3 | Halo : −3.0 <~ [Fe/H]<~ −1.0
Bulge : −0.5 <~ [Fe/H]<~ 0.5 |
| Rotation, km/s | Young disk: 220
Old disk : 180 - 200 |
Halo : 20 +/- 20
Bulge : circa 100 |
| Velocity Dispersion in (U,V,W) km/s | Young disk : (40, 30, 10)
Old disk : (80, 60, 20) |
Halo : (150, 100, 100)
Bulge : ~ 130 km/s |
We now turn to the topic of measuring ages for stars. After the mechanisms were discovered for providing stars with their energy (i.e. nuclear burning) it wasn't long before the effects of the energy source running out were also understood. The processes a star goes through during its lifetime are termed stellar evolution. (The term isn't a very good one, since evolution is more generally applied to large numbers of individuals in a species, and not to the individuals themselves.)
Ages can be measured for individual stars which have evolved slightly off
the main sequence (where they have spent most of their lives) but not yet moved
up the giant branch. This means F and G stars in practice --- they are the
only stars for which accurate ages can be obtained individually. Stars in
groups however, where a range of stars masses have all formed at the same time,
can be dated as a group. This is the case in open clusters and
globular clusters.
 |
 |
Most open clusters are young (less than 2 Gyr) and metal rich, move in
circular orbits around the Galactic center and have low velocity dispersion ---
hence they are Population I. Globular clusters are mostly distributed around
the Galactic disk in a spherical distribution, have large random velocities, no
or very little net rotation around the Galactic center and much less metal
content thatn the Sun (-2.5 < [Fe/H] < -1). These are archetypical
Population II objects (although a small subset is known to rotate
rapidly around the galaxy and have low velocity dispersion, like Population
I). A typical open cluster contains 100 to 1000 stars in is of order 1 to 10 pc
in radius. There are about 105 open clusters in the Galaxy (a very
loose number since the vast majority are hidden from view in the Galactic disk
behind dust clouds, or lost amongst all the foreground and background stars). A
typical globular cluster contains 104 to 106 stars. These
are much easier to find since they well away from the dust layer. There are
about 150 known, and probably about 200 in total.
Summary of cluster properties
| Globular Clusters | Open Clusters | |
| central density | circa 104 Mo pc-3 | circa 100 Mo pc-3 |
| core radius | 1.5 pc | 1 pc |
| median radius | 10 pc | 2 pc |
| tidal radius | 50 pc | 10 pc |
| central velocity dispersion | 7 km/s | 1 km/s |
| mass-to-light raio | 2 Mo / Lo | 1 Mo / Lo |
| typical mass | 5x105 Mo | 250 Mo |
| lifetime | 1010 years | 108 years |
Adapted from Binney and Tremaine, Table 1-3, page 26
The central density of stars in globular clusters is very high, about 10,000 solar masses per cubic parsec compared to only about 0.05 in the Solar neighbourhood. In the table, the core radius refers to the radius where the surface brightness falls to hald its central value; the median radius referes to the radius of a sphere which contains half of the total light, while the tidal radius is the point at which the gravitational field from the Galaxy is the same as the field of the cluster -- at this point stars can easily escape, and join the general background of field stars.
The key to aging a cluster is the colour-magnitude diagram. The colour of
the bluest stars on the main sequence (called the main sequence turnoff)
is directly related to the age of the cluster --- the older the cluster, the
redder the position of the turnoff.
Animation of stellar evolution click here
Note to self: mplayer -speed 0.01 /home/cflynn/frontpage/galdyn/HR.mpg
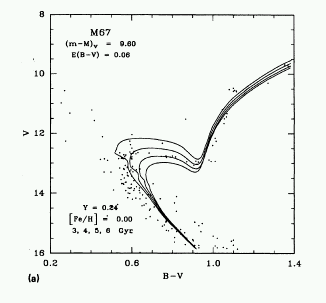
Open cluster colour magnitude diagrams are typically beset with the problems
that the clusters are contaminated with foreground and background stars, there
are not many stars in the cluster anyway, and the amount of dust
obscuration, metallicity and distance to the cluster have intrinsic
uncertainties. Various ways around these difficulties have been
developed, and most clusters can be dated to within +/- 30%.
There are much more stars in globular clusters, and deriving ages from isochrone fits is usually easier than in open clusters. The colour magnitude diagram for M92 is shown below: Four isochrones with ages of 12, 15, 18 and 21 Gyr are shown. Globular clusters are old, typically found to have ages in the range 12-15 Gyr.
Stellar evolution allows ages to be determined for these objects in a completely independent manner to the age determined for the universe from data such as distant supernovae, galaxy clustering and the microwave background. The current best age estimate for the Universe is 13.7 +/- 0.1 Gyr (from the WMAP mission). The errors in fitting ages to the best studies globular clusters are signifigantly larger than the WMAP error, and are typically at as uncertain as 1 Gyr. Thus we find, within the errors, good agreement in the two age estiamtes. Globular clusters are thought to be amongst the first stellar systems formed at all, but of course must be younger than the Universe as a whole!
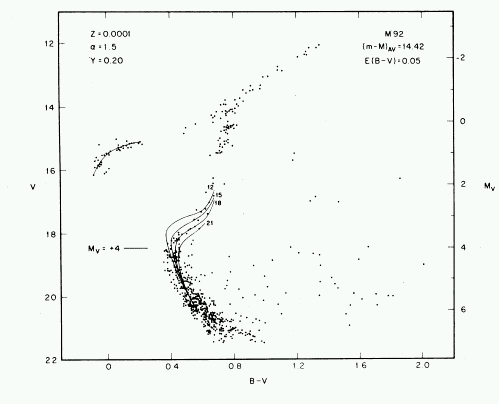
Colour magnitude diagram for the globular cluster M92. Source
http://adsabs.harvard.edu/cgi-bin/nph-bib_query?bibcode=1983AJ.....88.1159S
Original Source : Sandage, 1983, Astronomical Journal, 88, 1159
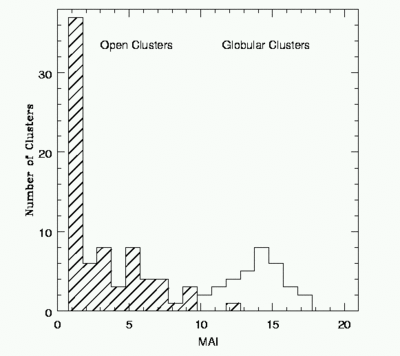
The following figure shows the distribution of ages (MAI - "mean age index"
in Gyr) for open and globular clusters, showing that most open clusters are
younger than 10 Gyr while Globular clusters are always at least this old. The
peak in the open clusters at young ages is because open clusters are not very
stable --- they are born and rapidly break up, dissolving into the stellar
field. Globular clusters, being much denser at having halo-like rather than
disk-like orbits are much more difficult to break up.
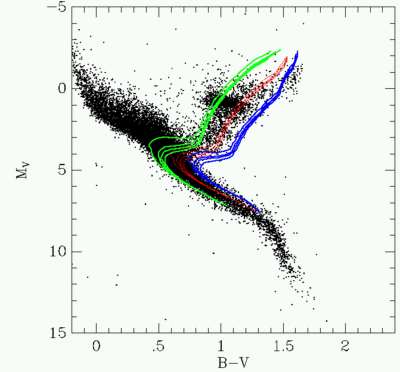
Colour magnitude diagram for nearby stars, with 3 "isochrones" of
differing age overlaid (and four different metallicities each). The oldest
stars in the disk have ages of about 10 Gyr. Source
preprint. Jimenez, Flynn and Kotoneva, 1998, MNRAS, 299, 515
As we have seen, the galaxy is thought to have collapsed from a cloud of primordial gas (whose composition was set essentially by the Big Bang) consisting of about 75% Hydrogen and 25% Helium plus a very small amount of the other elements (much less than 1%). As this cloud collapsed generations of stars were born. Each generation consists of many low mass stars which evolve slowly and are still with us today, and high mass stars which quickly spent their fuel and have since become white dwarfs, neutron stars or, possibly, black holes.
The stars that explode as supernovae at the end of their lives
distribute back into the primordial gas a large amount of heavy elements which
have been built up in the star via nucleosynthesis. As a result the
metallicity of the gas from which each new generation of stars forms rises
steadily, which results in correllations between the kinematics
(i.e. motions) of stars and their metallicities.
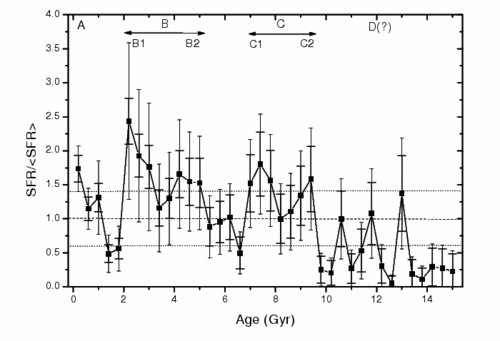
The plot above shows the rate at which stars have been forming in the solar neighbourhood, calculated by finding and measuring the ages of long-lived (low mass) stars near the Sun. Over the age range of 0 to 10 Gyr the amount of stars formed is roughly constant, with some bumps located at A, B and C where the formation rate seems to have been a bit above average. Beyond 10 Gyr many stars are missing and the determination is not reliable.
As these stars formed there has been a generally rising metallicity, although with a great deal of scatter. Older textbooks will speak of a quite good relationship between metallicity and age (called the AMR or Age-Metallicity Relation). Studies within the last decade have shown that this relationship is much weaker and contains more intrinsic scatter than previously thought.
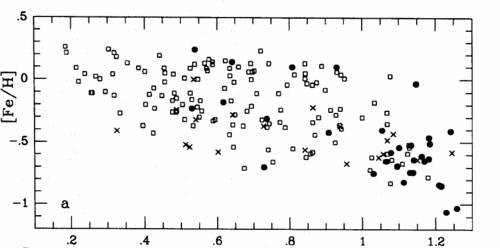
Source : Edvardsson
et al 1993
There is a much clearer relation than the AMR, which is the one between
stellar age and kinematics (or velocities) of the stars.
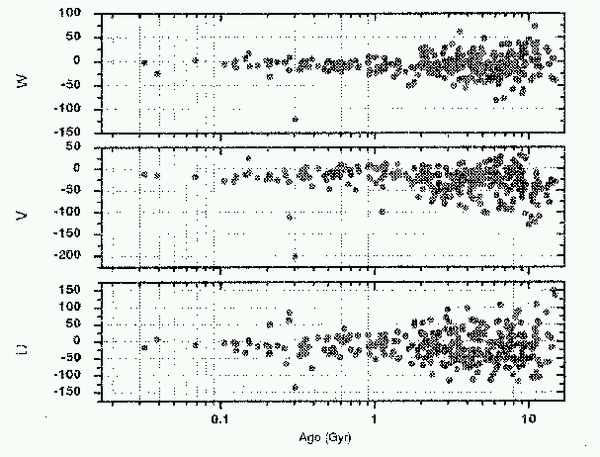
The velocity of stars in the Galactic coordinate frame (U, V, W), shown as a function of the star's age, in Gyr (note logarithmic scale). Young stars have a significantly lower velocity dispersion than older stars. Source : Rocha-Pinto et.al. Preprint, 1999.
The plot shows (U, V, W) velocities of G and K dwarf stars near the Sun for which an age has been measured. Note that young stars generally have much smaller velocities than old stars (> approx 1 Gyr). Young stars have recently been born from gas clouds and their low velocities constrain them to movements within a few 100 parsecs of the Galactic plane. Older stars have had time for their orbits to be changed by encounters with irregularities in the disk of the Galaxy, such as spiral arms and giant molecular clouds, and show much larger random motions and a larger scale height. This diagram shows why the dividing line between the young and the old disk is set at about 1-2 Gyr.
| Exercise #2: the velocities of the stars are symmetric around U=0 and W=0, but are not symmetrically distributed around V=0. What's going on here? A clue may be had in the fact that the V velocities of the youngest stars do appear to be symmetric around V=0. |
A great deal of work has gone into this issue over the last 30 years and has led to the conclusion that the visible parts of galaxies represent only a small part of the total mass of the galaxy. Most of the mass in galaxies seems to be in a dark form, the composition of which still remains completely uncertain. We now know that about 85 percent of the mass of galaxies, and indeed the cosmos, is in this dark form. In other words, we don't know what the major part of the universe is made of!
The main evidence for dark matter comes from rotation curves of disk galaxies. A rotation curve measures the rate at which stars and/or gas move in their circular orbits around the center of the galaxy.
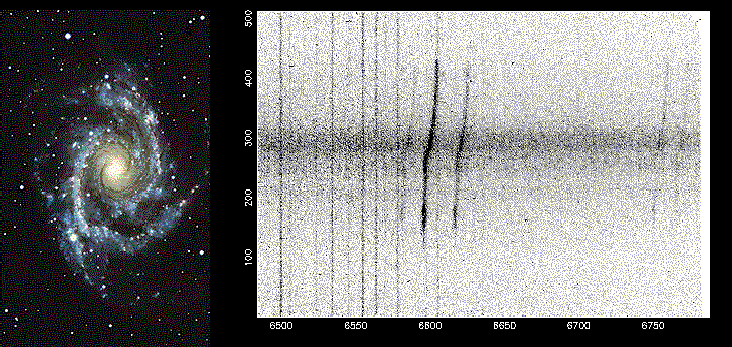
| Exercise #3: estimate from the plot the wavelength of the line (the scale is in Angstroms, and runs from 6500 to 6750) from the central regions of the galaxy --- this will allow you to estimate the galaxy's redshift. Now estimate how fast the upper and lower parts of the galaxy are moving relative to the center. The difference is a measure of how fast the galaxy is rotating. Finally, construct a plot of the rotation rate of the galaxy as a function of distance from the center. How fast are the outer parts of the galaxy rotating? |
The exercise above will result in a so-called rotation curve of the galaxy, and shows how fast gas and stars are moving around the center of the galaxy, as a function of distance from the center.
The rotation curve of the milky way is much harder to measure than for external galaxies, since the gas and stars beyond the solar circle are moving mostly transverse to the line-of-sight rather than along it. However, so many rotation curves have been measured for other disk galaxies there is no reason to suppose that the Milky Way would be particularly different, so even if the flattness of the rotation of the outer Galaxy is poorly measured it is thought to be flat nevertheless. Improved astrometric space missions within a decade or two will resolve this observational difficulty.
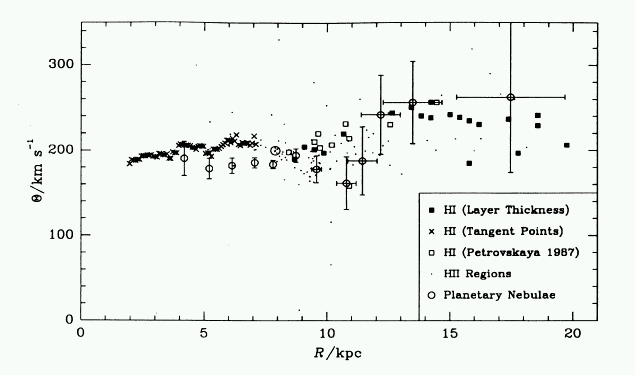
One can see from the figure that the Sun (which is at a distance of about 8 kpc from the center) moves at about 220 km/s in a circular orbit around the center of the galaxy, like almost all the stars near the Sun.
We can estimate the amount of matter inside the Sun's orbit by assuming that all the matter is at the Galactic center, a not too bad approximation.
Let the speed be V0 , the mass of the Galaxy be MG and the distance of the Sun from the Galactic center be R0. The centrifugal force due to rotational speed must balance the gravitational force due to the mass of the Galaxy, so that:
GMGal/R02 = V02/R0
where G is the gravitational constant.
Hence
MGal = V02 R0/G
substituting values of 8 kpc and 220 km/s for the Sun and G = 0.00430 M0 (km/s)2 / pc, we get
MGal(R<8) = 1011 M0
This is an estimate of the amount of matter inside 8 kpc.
This is within an order of magnitude of the mass determination of 6 x 1011 M0 obtained by more realistic modelling of the disk, showing that the approximation is not too bad.
As the curve shows, measurements of the rotation of the outer edge of the Milky Way show that the stars out there also rotate at 220 km/s, out to about 20 kpc.
Thus, within the radius of 20 kpc we get a mass of
MGal(R<20) = 2x1011 M0.
A flat rotation curve, in which the velocity doesn't fall with increasing distance from the center of the galaxy, implies that the amount of matter enclosed increases slowly with radius.
The surprise comes when we compare how the amount of enclosed light behaves. As we saw in the previous lecture, the disks of spiral galaxies are closely fit by an exponential distribution. For the Milky Way, the scale length is about Rh = 3 kpc. In other words, the density ρ of stars (and light) decrease with distance R like
ρ = ρ(0) exp (-R/Rh).
Knowing the light distribution, we can compute how much light is emitted by the region inside 8 kpc, compared to the region inside 20 kpc. The amount of light inside 20 kpc comes out to be only 30% greater than the amount inside 8 kpc. Remember that the amount of mass inside 20 kpc was twice the amount inside 8 kpc.
The conclusion is that the distribution of emitted light is not necessarily the same as the underlying distribution of matter.
Unless our theories of gravity are wrong, there is matter in these galaxies which we cannot see. The matter is termed "dark", and sometimes also called "missing matter", although a better name would be "missing light".
Studies of rotation curves of other galaxies (the Milky Way is particularly difficult to study in this way because of peculiarities concerning our position within it) have shown that there is a lot of matter in galaxies which we cannot see, outweighing the visible matter (i.e. stars and gas) by about 6 to 1.
More on dark matter later in the course!