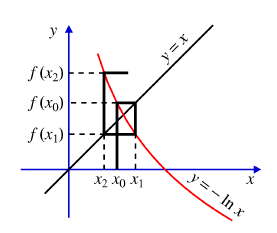
 Esimerkiksi yritetään ratkaista yhtälö x = -ln x.
Arvataan x0 = 0.5 ja lasketaan
Esimerkiksi yritetään ratkaista yhtälö x = -ln x.
Arvataan x0 = 0.5 ja lasketaan
| kotisivu |
| hakemisto |
| kartat |
| kohteet |
| teoriaa |
| matematiikkaa |
f(x) = x.
Arvataan jokin likiarvo ratkaisulle tai arvioidaan se graafisesti. Merkitään tätä lähtöarvoa x0:lla. Lasketaan x1 = f(x0), x2 = f(x1), jne, kunnes peräkkäiset x:n arvot eroavat vähemmän kuin tarkkuudelle asetettu vaatimus. Viimeinen x:n arvo on tällöin yhtälön ratkaisu. Kun muutama ensimmäinen x:n arvo on laskettu, nähdään alkavatko ne supeta. Mikäli x:n arvot rupeavat hajaantumaan, ei kannata jatkaa, vaan muutetaan yhtälö muotoon
f-1(x) = x
ja yritetään uudestaan. f-1 on f:n käänteiskuvaus.
 Esimerkiksi yritetään ratkaista yhtälö x = -ln x.
Arvataan x0 = 0.5 ja lasketaan
Esimerkiksi yritetään ratkaista yhtälö x = -ln x.
Arvataan x0 = 0.5 ja lasketaan
x1 = -ln 0.5 = 0.69,
x2 = 0.37,
x3 = 1.00.
Tästä jo nähdään, että eihän hommasta mitään tule.
Kirjoitetaan yhtälö muotoon x = e-x ja aloitetaan alusta:
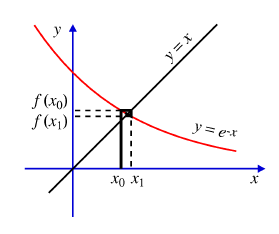 x0 = 0.5,
x0 = 0.5,
x1 = e-0.5 = 0.61,
x2 = 0.55,
x3 = 0.58,
x4 = 0.56,
x5 = 0.57,
x6 = 0.57.
Kahden desimaalin tarkkuudella ratkaisu on siis
0.57.
Ratkaistaan edellä ollut yhtälö tällä menetelmällä. Yhtälö on nyt f(x) = 0, missä f(x) = x + ln x. Koska f(x) lähestyy -ääretöntä, kun x -> 0, ja f(1) > 0, on ratkaisu välillä (0,1). Lasketaan f(0.5)< 0, joten ratkaisu x on välillä (0.5, 1). Jatketaan tällä tavoin:
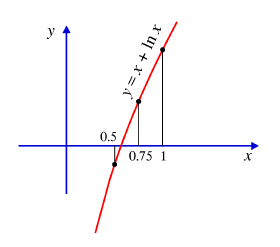
f(0.75) > 0 =>
0.5 < x < 0.75,
f(0.625) > 0 =>
0.5 < x < 0.625,
f(0.563) < 0 =>
0.563 < x < 0.625,
f(0 594) > 0 =>
0.563 < x < 0.594,
Suppeneminen on hidasta, mutta varmaa.