kotisivu
hakemisto
kartat
kohteet
teoriaa
matematiikkaa

Trigonometriaa

Trigonometria tarkoittaa kolmion mittausoppia. Siihen liittyvät trigonometriset funktiot on alkuaan määritelty suorakulmaisen kolmion sivujen suhteina. Niitä voidaan pitää myös yleisinä funktioina, joilla on laajempaakin käyttöä.

Trigonometriset funktiot

Kulmiin liittyvät trigonometriset funktiot määritellään usein suorakulmaisen kolmion sivujen suhteina. Tämä tapa soveltuu kuitenkin vain kulmille, jotka ovat välillä 0°-90°. Ne voidaan määritellä myös toisella tavalla, joka sopii kaikille kulmille. Itse asiassa tämä tapa on helpommin muistettava kuin se kolmioihin perustuva.

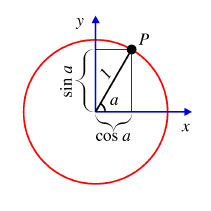Piirretään aluksi suorakulmainen xy-koordinaatisto. Sen akselien leikkauspisteeseen piirretään ympyrä, jonka säde on 1. Viereisen kuvan mukaisesti mitä tahansa x-akselista vastapäivään mitattua kulmaa a vastaa aina yksikäsitteinen piste P ympyrän kehällä. Määrittelemme nyt, että kulman a kosini on pisteen P x-koordinaatti, ja sini sen y-koordinaatti. Kulman tangentti määritellään sitten sinin ja kosinin avulla: tan a = sin a / cos a eli tan a = y / x.

Soveltamalla kuvan kolmioihin Pythagoraan lausetta saadaan välittömästi tärkeä yhteys sinin ja kosinin välille:

sin2a + cos2a = 1.

Kuvasta nähdään, että sini on pariton ja kosini parillinen funktio:

sin (- a) = - sin a
cos (- a) = cos a

Molemmat ovat jaksollisia funktioita:

sin (a + n 360°) = sin a
cos (a + n 360°) = cos a,

missä n on mikä tahansa kokonaisluku (positiivinen tai negatiivinen).

Kuvasta voidaan myös helposti lukea trigonometristen funktioiden arvoja joissakin erikoispisteissä:

kulma sin cos tan
0° 0 1 0
90° 1 0 ääretön
180° 0 -1 0
270° -1 0 -ääretön

Seuraavassa on lueteltu vielä yhteenvetona trigonometristen funktioiden määritelmät. Mukana on myös joitakin vähemmän käytettyjä funktioita, joita saattaa tavata varsinkin vanhemmassa kirjallisuudessa.

sini sin a = y
kosini cos a = x
tangentti tan a = y/x = sin a / cos a
kotangentti cot a = x/y = cos a / sin a
sekantti sec a = 1 /x = 1 / cos a
kosekantti csc a = 1 /y = 1 / sin a
versini vers a = 1 - x = 1 - cos a
koversini covers a = 1 - y = 1 - sin a
haversini hav a = (1 - x) / 2 = (1 - cos a)/2 = (1/2) vers a
eksekantti exsec a = 1 /x - 1 = sec a - 1

Käänteisfunktiot

Usein tarvitaan myös trigonometristen funktioiden käänteisfunktioita. Tiedämme siis kulman sinin, kosinin tai tangentin, ja sen avulla on laskettava kulma. On siis ratkaistava x esimerkiksi yhtälöstä

cos x = c.

Tällä on kuitenkin ääretön määrä ratkaisuja. Jos nimittäin a toteuttaa yhtälön, sen toteuttavat myös -a, a+360°, a-360° jne.

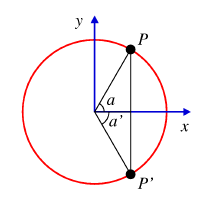Jos esimerkiksi kulman kosini on 0.5, kuten oheisessa kuvassa, voi sitä vastaava piste ympyrän kehällä olla joko x-akselin ylä- tai alapuolella. Kulma voi siten olla a = 60° tai a' = -60° = 300°. Se voi olla tietysti myös 420°, 660° 780° jne.

Jotta ratkaisu olisi yksikäsitteinen, se on rajoitettava sopivalle välille. Kosinin tapauksessa sopiva väli on 0° .. 180°. Kun rajoitutaan tälle välille, yhtälön ratkaisu voidaan esittää muodossa

x = arc cos c,

missä arc cos on kosinin käänteisfunktio. Vastaavasti sinin käänteisfunktio on arc sin ja tangentin arc tan. Oikeastaan kysymyksessä on käänteisfunktion ns. päähaara.

Ohjelmointikielten funktio arccos tai acos samoinkuin laskinten cos-1 antaa yleensä juuri päähaaran arvon, eli sen kulman, joka on välillä 0°-180°. Vastaavasti funktion arcsin tai asin antama kulma on välillä -90°- +90°.

Mikäli kulman sini ja kosini tunnetaan, kulma voidaan ratkaista yksikäsitteisesti. Samoin jos pisteen x- ja y-koordinaatit tiedetään, kulma saadaan aina yksikäsitteisesti. Tähän tarkoitukseen kätevin keino on ohjelmointikielten funktio arctan2 tai atan2, jonka kutsu voi olla esimerkiksi muotoa atan2(y,x). Kun x:n arvoksi asetetaan kulman kosini (tai x-koordinaatti) ja y:n arvoksi kulman sini (tai y-koordinaatti), palauttaa atan2 arvonaan juuri oikean kulman. Laskimissa on usein samaan tehtävään soveltuva funktio R -> P, joka muuntaa suorakulmaiset koordinaatit napakoordinaateiksi. Taaskin x:ksi asetetaan kulman kosini ja y:ksi sen sini. Funktio R -> P palauttaa sitten sekä kulman että pisteen etäisyyden.

Sekalaisia kaavoja

Yhteenlaskukaavat:

sin (a + b) = sin a cos b + cos a sin b
sin (a - b) = sin a cos b - cos a sin b
cos (a + b) = cos a cos b - sin a sin b
cos (a - b) = cos a cos b + sin a sin b
tan (a + b) = (tan a + tan b) / (1 - tan a tan b)
tan (a - b) = (tan a - tan b) / (1 + tan a tan b)

Kun näissä asetetaan b = a, saadaan kaksinkertaisen kulman kaavat:

sin 2a = 2 sin a cos a
cos 2a = cos2a - sin2a = 2 cos2a - 1 = 1 - 2 sin2a
tan 2a = 2 tan a / (1 - tan2a )

Kolmion ratkaisukaavat

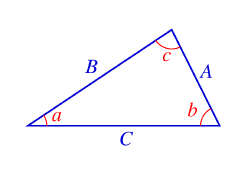Merkitään kolmion kulmia pienillä kirjaimilla (a, b, c) ja niiden vastaisia sivuja vastaavilla isoilla kirjaimilla (A, B, C).

Sinikaava:

A / sin a = B / sin b = C / sin c

Kosinikaava:

A2 = B2 + C2 - 2 BC cos a

Jälkimmäinen on Pythagoraan lauseen yleistys mielivaltaiselle kolmiolle.