Almagestin matematiikkaa
Almagestin uusissa käännöksissä käytetään
numeroille nykyaikaista notaatiota.
Kreikkalaisilla ei ollut käytössään
varsinaisia numeroita, vaan he esittivät
luvut kirjainmerkeillä.
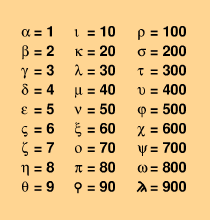 Muut luvut saadaan yhdistelemällä näitä
merkkejä. Esimerkiksi sigma-ny-gamma=253.
Varsinaisten kreikkalaisten kirjainten lisäksi
joukossa on esitystavasta riippuen 2-3
merkkiä, jotka ovat peräisin
kreikankielen vanhemmasta foinikialaisiin
aakkosiin perustuvasta kirjaimistosta.
Näiden ohella Almagestissä esiintyy nollaa esittävä
merkki (o-kirjain, jonka päällä on viiva)
sekä joukko ykköstä pienempiä
murtolukuja tarkoittavia merkkejä, jotka
tunnistaa kirjaimen päällä olevista heittomerkeistä.
Muut luvut saadaan yhdistelemällä näitä
merkkejä. Esimerkiksi sigma-ny-gamma=253.
Varsinaisten kreikkalaisten kirjainten lisäksi
joukossa on esitystavasta riippuen 2-3
merkkiä, jotka ovat peräisin
kreikankielen vanhemmasta foinikialaisiin
aakkosiin perustuvasta kirjaimistosta.
Näiden ohella Almagestissä esiintyy nollaa esittävä
merkki (o-kirjain, jonka päällä on viiva)
sekä joukko ykköstä pienempiä
murtolukuja tarkoittavia merkkejä, jotka
tunnistaa kirjaimen päällä olevista heittomerkeistä.
Nuolenpääkirjoituksissa käytettiin johdonmukaista
60-kantaista esitystapaa. Ptolemaios käyttää sitä
vain luvun ykköstä pienemmälle osalle. Esimerkiksi
110.5 on rho-iota-lambda eli 100+10
kokonaista ja 30 kuudeskymmenesosaa.
Nuolenpääkirjoituksissa myös kokonaisosa olisi
esitetty 60-kantaisella paikkamerkinnällä: 1 50 30.
Myöhempinä aikoina kulmien sekunteihin alettiin
vielä liittää desimaaliosia, minkä tuloksena
syntyivät sellaiset kolmea eri esitystapaa
sisältävät sekasikiöt kuin 110° 29' 55,1".
Ptolemaioksen käyttämällä merkintätavalla lienee
ollut merkittävä vaikutus siihen, että se jäi
yleiseen käyttöön kulmayksiköiden yhteydessä. Jos
haluamme Ptolemaiosta syyttää jostakin, oikea
kohde on tämä tarpeettoman hankala merkintätapa, joka
pysynee vaivanamme vielä pitkään. Tosin suurempia
syyllisiä ovat taaskin jälkipolvet, jotka aina
vain pitävät kiinni perinteistä, vaikka ne
olisivat miten hölmöjä tahansa.
Kirjan I alussa Ptolemaios perustelee
perusolettamuksiaan, joiden mukaan
Maa on pallomainen ja liikkumaton sekä
sijaitsee maailmankaikkeuden keskipisteessä.
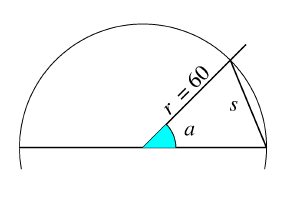 Kirjassa I esitellään myös muutamia geometrisia
aputuloksia. Yhtä niistä voidaan pitää
jonkinlaisena trigonometrian edeltäjänä. Jos
sijoitamme kulman a ympyrän keskelle,
kulman sivut leikkaavat ympyrän kehän kahdessa
pisteessä. Näitä pisteitä yhdistävän
janan pituutta voimme kutsua kulman a
jänteeksi. Jos kiinnitämme ympyrän säteen,
kulmat ja jänteet vastaavat toisiaan täysin
yksikäsitteisellä tavalla.
Kirjassa I esitellään myös muutamia geometrisia
aputuloksia. Yhtä niistä voidaan pitää
jonkinlaisena trigonometrian edeltäjänä. Jos
sijoitamme kulman a ympyrän keskelle,
kulman sivut leikkaavat ympyrän kehän kahdessa
pisteessä. Näitä pisteitä yhdistävän
janan pituutta voimme kutsua kulman a
jänteeksi. Jos kiinnitämme ympyrän säteen,
kulmat ja jänteet vastaavat toisiaan täysin
yksikäsitteisellä tavalla.
Almagestin I kirjassa Ptolemaios kertoo
jakavansa ympyrän halkaisijan 120 osaan.
Ympyrän säde on siis 60 yksikköä.
Käytetään kulmaa a vastaavalle
jänteelle merkintää chd a. Jänteen
pituus on silloin
chd a = 2 r sin (a/2) = 120 sin (a/2).
Tämä on siis yhteys, joka liittää
toisiinsa Ptolemaioksen jänteet ja
nykyisin käytetyt trigonometriset funktiot.
I kirjassa Ptolemaios taulukoi kulmia
vastaavat jänteet puolen asteen välein.
Kyseessä on siten trigonometristen taulukoiden
edeltäjä. Lisäksi kunkin kulman jälkeen
on laskettu, kuinka paljon jänne kasvaa
kulman kasvaessa 1/60 astetta. Näiden
lukujen avulla on helppo
interpoloida
jänteen pituus niille kulmille, jotka eivät
satu olemaan täysiä puolia asteita.
Menetelmää käytetään nykyisinkin monissa
taulukkoteoksissa.
Kaikkien näiden jänteiden laskeminen lähtemällä
geometrisista konstruktioista olisi hirvittävä
urakka. Siksi Ptolemaios todistaakin aluksi
muutamia aputuloksia. Nykyaikaisemmalla
merkintätavalla voimme esittää nämä siten,
että jos chd a ja chd b
tunnetaan, chd (a - b),
chd (a + b) ja chd a/2
voidaan laskea.
Esimerkiksi kuusikulmion sivua vastaava
kulma on 60°. Puolittamalla tätä
saadaan kulmia 30° ja 15°
vastaavat jänteet. Viisikulmiosta puolestaan
saadaan kulmia 72°, 36°, 18°
vastaavat jänteet. Edelleen 18°-15°=3°,
josta saadaan 1 1/2 ° vastaava jänne.
Lisäämällä puoltatoista astetta itseensä
voidaan laskea kaikkia sen monikertoja
vastaavat jänteet. Väliin jää kuitenkin
vielä joukko kulmia, joita vastaavien jänteiden
laskeminen ei onnistu tällä tavalla. Ptolemaios
tyytyykin johtamaan riittävän tarkan arvion
puolta astetta vastaavalle jänteelle. Tämän
ja jo laskettujen jänteiden avulla voidaan
loputkin jänteet laskea.
Almagestin II kirjassa yleisen teorian käsittely
jatkuu. Se on esitys pallotrigonometrian ja
pallotähtitieteen yleisistä perusteista.
Luku kattaa suunnilleen samat asiat kuin
tähtitieteen yliopistollisen peruskurssin
pallotähtitieteen osuus
II kirja käsittelee erityisesti päivän
pituutta eri leveyksillä. Pohjoisimmat
leveydet, joista annetaan muutakin kuin
tähtitieteellistä tietoa, ovat:
xxix. Ja missä pisin päivä on 20 ekvatoriaalista
tuntia, siellä leveyspiiri on 63° ekvaattorista
ja kulkee Thulen saaren kautta.
xxx. Ja missä pisin päivä on 21 ekvatoriaalista
tuntia, siellä leveyspiiri on 64 1/2 °
ekvaattorista ja kulkee tuntemattomien
skyyttien maiden kautta.
Skyyttien alue alkoi Mustan meren
pohjoispuolelta ja jatkui jonnekin syvälle
pohjoiseen. Ptolemaios oli tunnettu
maantieteilijänäkin, mutta näköjään
hänkään ei ollut perillä, millaista väkeä
Suomen leveyksillä asui. Tuskin skyyttien
alue näin kauas sentään ulottui.
Tästä pohjoiseen maapallo olikin sitten
täysin terra incognita.
Ptolemaios toki kuvaa Auringon liikkeen oikein eri
leveyksillä aina pohjoisnavalle saakka.
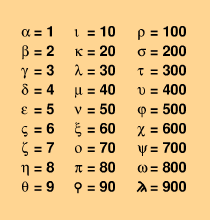 Muut luvut saadaan yhdistelemällä näitä
merkkejä. Esimerkiksi sigma-ny-gamma=253.
Varsinaisten kreikkalaisten kirjainten lisäksi
joukossa on esitystavasta riippuen 2-3
merkkiä, jotka ovat peräisin
kreikankielen vanhemmasta foinikialaisiin
aakkosiin perustuvasta kirjaimistosta.
Näiden ohella Almagestissä esiintyy nollaa esittävä
merkki (o-kirjain, jonka päällä on viiva)
sekä joukko ykköstä pienempiä
murtolukuja tarkoittavia merkkejä, jotka
tunnistaa kirjaimen päällä olevista heittomerkeistä.
Muut luvut saadaan yhdistelemällä näitä
merkkejä. Esimerkiksi sigma-ny-gamma=253.
Varsinaisten kreikkalaisten kirjainten lisäksi
joukossa on esitystavasta riippuen 2-3
merkkiä, jotka ovat peräisin
kreikankielen vanhemmasta foinikialaisiin
aakkosiin perustuvasta kirjaimistosta.
Näiden ohella Almagestissä esiintyy nollaa esittävä
merkki (o-kirjain, jonka päällä on viiva)
sekä joukko ykköstä pienempiä
murtolukuja tarkoittavia merkkejä, jotka
tunnistaa kirjaimen päällä olevista heittomerkeistä.
 Kirjassa I esitellään myös muutamia geometrisia
aputuloksia. Yhtä niistä voidaan pitää
jonkinlaisena trigonometrian edeltäjänä. Jos
sijoitamme kulman a ympyrän keskelle,
kulman sivut leikkaavat ympyrän kehän kahdessa
pisteessä. Näitä pisteitä yhdistävän
janan pituutta voimme kutsua kulman a
jänteeksi. Jos kiinnitämme ympyrän säteen,
kulmat ja jänteet vastaavat toisiaan täysin
yksikäsitteisellä tavalla.
Kirjassa I esitellään myös muutamia geometrisia
aputuloksia. Yhtä niistä voidaan pitää
jonkinlaisena trigonometrian edeltäjänä. Jos
sijoitamme kulman a ympyrän keskelle,
kulman sivut leikkaavat ympyrän kehän kahdessa
pisteessä. Näitä pisteitä yhdistävän
janan pituutta voimme kutsua kulman a
jänteeksi. Jos kiinnitämme ympyrän säteen,
kulmat ja jänteet vastaavat toisiaan täysin
yksikäsitteisellä tavalla.