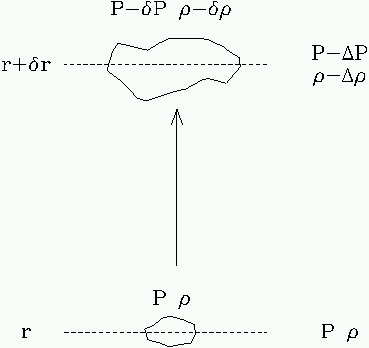
So far we have only considered the transport of energy out of the star by radiation. For low mass stars, another very important mechanism exists, that of convection. Convection involves the physical transport of heat by the rising and falling of gaseous elements. Consider a small gas blob at pressure P and with density r. If the blob rises slightly in the star, so that there is no need to consider heat exchange with the surrounding elements (i.e. the change takes place adiabatically, then
| (1) |
where g is the ratio of the specific heats at constant pressure CP to constant volume, CV
| (2) |
If the change takes place so that the the gas blob finds itself in a region where its bouyancy is positive (i.e. its density is lower than the density of the surrounding gas) then it will continue to rise. Let the blob begin at radius r in the star, with density r and internal pressure P, in a surrounding medium at the same density and pressure, as shown in figure 9.1. The blob rises slightly, to a radius r + dr, and acquires a a new density r- dr and pressure P-dP. The surrounding medium has a different change in density and pressure with radius, denoted r-Dr and P-DP (see figure 9.1). Now, if
| (3) |
the gas blob will continue to rise, causing energy transfer by convection (otherwise the blob will just be forced back to where it came from and convection will not occur).
Convective blobs rise much slower than the local sound speed, so that pressure differences between the blob and the surrounding medium will be small, i.e.
| (4) |
From Eqn 9.1 we thus obtain
| (5) |
or
| (6) |
For small dr, we get
| (7) |
and thus
| (8) |
We can use pressure to track the motion of the blob just as well as the radius, and since the pressure difference between the blob and the surroundings is considered negligible, our condition for convection is just
| (9) |
|
Show that the convection criterion can also be written
|
The ratio of the specific heats, g, is thus a very important parameter in determining instability to convection. For an ideal gas, g = 5/3.

Convection can take place of the pressure gradient is low enough or the temperature gradient is high enough.
In the first case, we are looking for conditions under which the plasma can absorb energy without the temperature increasing (such as occurs at a phase change). Such conditions exist where the primary constituents, H and He are being ionised by energy input rather than increasing their kinetic energy (temperature). As a result, the specific heat at constant volume is high, and g is small. As we saw in the last lecture, H ionisation takes place at circa 10,000 K and He ionisations take place at about 20,000 K and 50,000 K. We therefore find convection in the outer layers of the Sun.
In the second case, we can make use of the expression for the luminosity in terms of the temperature gradient and the opacity, under the condition of outward radiative energy transport:
| (12) |
and hence
| (13) |
The pressure gradient is given by the hydrostatic equation, which can be show to have the form
| (14) |
where m is the mean atomic weight and Rg is the gas constant, and g is the local gravitational acceleration in the star. From this one can obtain an expression for Ñrad
| (15) |
where
| (16) |
This relation shows that convection can be expected if the flux F or the opacity k is large at a given temperature T. Such conditions can occur in stellar cores if sufficient energy is being produced, as is the case in high mass stars. This leads to core convection, which has important consequences for stellar evolution (see next lecture), because it allows a larger fraction of the material to be burnt in the core than would otherwise be the case.
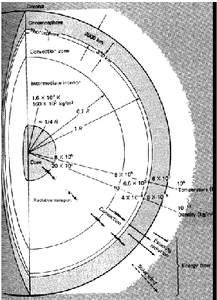
Convection occurs when the opacity is high enough. Deeper down than the He and H ionisation layers (the ionisation energy of which leads to convection in the very outer layers of the Sun, as described in the previous section), small amounts of the metals in the Solar mix still retain electrons and contribute to the opacity. There is opacity of this type up to temperatures of a few million degrees for enough heat to be trapped and lead to convection preferentially transfering the heat outwards. For the Sun, this takes place in the outer 30% of the radius (see figure 9.2).
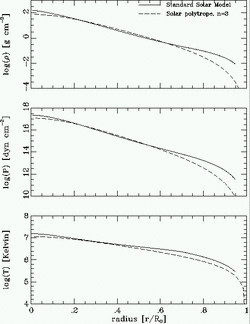
To summarise, cool stars have deep convective envelopes, while hotter stars have thinner convection zones and wide radiative zones. Very cool M dwarfs can be fully convective, i.e. the convection zone reaches all the way to the center (see figure 9.5). Furthermore, massive stars may have convective cores, an important consequence for their evolution. Convection is a complicated topic and reamins an active area of research, in particular because it can have considerable impact on a wide range of stellar properties and stellar evolution. The lack of a good theory of convection, and the amount of energy which can be transfered by convection, is at present a limitation on our understanding of stellar structure.
|
|