In all directions, the view we have of the Universe is very similar - on large scales. The view of the Universe is said to be isotropic. There are many examples of this: the distribution of gamma-ray bursters, the distribution of quasars, faint radio sources and the microwave background.
On small scales, less than clusters of galaxies, the Universe is manifestly not uniform. Objects exist, including ourselves! In cosmology such structure is ignored - we are concerned only with treating the Universe as a kind of fluid. The questions one can ask are very straightforward. Is it infinite or finite in time and space? If finite in time, how old? If finite in space, how big? Like medieval explorers of the Earth's surface, one can ask if it is flat or curved, even closed (like the Earth's surface). What is its average density of matter? How does the gravity of this matter control its destiny? What will happen to it in the long run?
The night time sky is dark. This seemingly simple statement has profound consequences in cosmology: one way to interpret it is that the Universe has a finite age.
The intensity Is of a source falls as the inverse square law,
| (1) |
If sources of radiation are uniformly spread around us in space, then their number N increases with the distance r squared,
| (2) |
The inverse square law of radiation thus implies that the total intensity I of sources of intensity Is, out to a distance R, increases uniformly,
| (3) |
If the universe is infinite in extent (R ® ¥)) then its luminosity should also be infinite. This derivation ignores the physical size of the sources generating the luminosity, which in practice will eventually eclipse the light from more distant sources. The practical limit then is the surface brightness of the source. If the Universe were filled with homogeneously distributed stars like the Sun, the night sky would be as bright as the Sun!
The simplest interpretation of the darkness of the night sky is that the Universe is of finite age, T, and light from regions more distant than the light travel time cT has not yet reached us. Another interpretation is that the universe is infinite but expanding, causing the light intensity from distant regions to fall faster than the inverse square law.
Three observations conspire together to suggest that the Universe has a finite age.
The basic working assumption in cosmology is termed the ``cosmological principle''. It states that the Universe, as seen by observers anywhere in it looks homogeneous and isotropic. There is no preferred position in the Universe. The philosophical basis for this assumption can be traced back to the ``Copernican principle'', which cast out the Earth-centered view of the Universe, and eventually dethroned the Sun and the Galaxy from central positions in the cosmos. Ultimately, this principle codifies a kind of healthy optimism on our own part - since it allows us to attempt to recover the properties of the Universe from a single vantage point here on Earth.
Newtonian gravitation and concepts of space and time can be used to construct an (almost) self-consistent model of the cosmos, which satisfies the cosmological principle.
Let the Universe consist of a homogeneous and isotropic fluid of density r(t), and consider a mass m at a distance r from a point O.
If we let the Universe expand by a factor R(t) as a function of time, then the radius will scale from r0, say, to r as
| (4) |
The velocity is v = [r\dot], so
| (5) |
where we have set H = [ [R\dot]/R]. This is called the Hubble parameter and measures the ``expansion rate'' of the Universe. The present value of the Hubble parameter is the Hubble constant:
| (6) |
The only motion permitted if the cosmological principle is to be retained is uniform expansion or contraction of this type.
An energy conservation equation for the system can be written down: it is called the Friedmann equation. We require constancy of kinetic and potential energy,
| (7) |
The constant depends on the adopted metric of the space-time in General Relativity, expressed in the most general metric which satisfies the cosmological principle, due to Robertson-Walker:
| (8) |
Thus k is the curvature constant. If k ¹ 0, one may redfine the scale of r so that k = ±1. We thus have values of k = -1, 0, 1 at our disposal in constructing a cosmology. k = 1 represents positively curved (elliptical) space, k = 0 flat space and k = -1 negatively curved (hyperbolic) space. Flat Universes have exactly the right density so that they continue to expand forever - this density is called the critical density and is denoted W0.
We can define the deceleration parameter, q0 as
| (9) |
and the density parameter
| (10) |
|
Problem 12.1 Show that
and
|
There are a number of solutions to Eqn 12.7. We'll concentrate here on those that are part of the standard cosmological model, in which the Universe began in a hot dense state and is presently expanding. One such solution is the Einstein-de Sitter model,
| (13) |
|
Problem 12.2 Show this is a solution to Eqn. 12.7.
|
Such a universe expands monotonically, but at an ever decreasing rate, as it is slowed down by the matter.
For k = -1, we see that [R\dot] > 0 at all times. R thus increases monotonically. These solutions are initially like the Einstein-de Sitter one but approach asymptotically a uniform expansion rate which continues forever.
For k = 1, there will be value of R at which the expansion will stop, [R\dot] = 0.
| (14) |
This leads to a contraction of the model, and eventually a ``big crunch''. The amount of matter in the model is what controls their development. For a critical density universe, W0 = 1. If the density of the universe is less than the critical density, the model re-collapses, otherwise it expands forever.
All of these Universes of the ``big bang'' type: they all have R = 0 in the past, at which time the Universe is ``born'' with infinite density.
Let us consider what happens to the radiation in the Universe if we trace its expansion backward in time. Photons are unaffected by other forces of nature, and so the wavelength of the radiation scales as R(t). For blackbody radiation,
| (15) |
and so T µ R(t)-1.
The radiation energy density U µ T4, and so U µ R(t)-4. If we regard this as a mass density in the radiation rt, then
| (16) |
|
Problem 12.3 What is the present day radiation density in the Universe for a microwave background temperature of 3 K? What is this as a mass density? How does it compare to the density of matter in the Universe?
|
On the other hand, the mass density, rm assuming no matter is created or destroyed, scales with the inverse of the volume,
| (17) |
This leads to a very important result - at some time in the past the radiation density will be greater than the matter density, no matter how small the ration is presently. These two regimes are called the radiation dominated and the matter dominated epochs.

Adopting a (flat) Einstein-de Sitter universe, R(t) = R0(t/t0)2/3, an age t and present day temperature of the Universe, T0, we can solve for the temperature as a function of time,
| (18) |
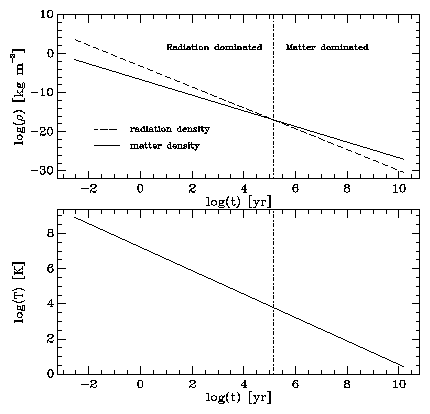
The temperature evolution is shown in figure 12.1 as a function of time. The temperature rises from the present day value of 2.7 K as we go back in time, reaching ~ 104 K approximately 100,000 years after the big bang. This temperature is high enough to ionise the matter: prior to this time the free electrons will strongly scatter the radiation, whereas after it the matter hardly interacts with the radiation. This is the surface of last scattering small irregularities in which tell us a great deal about the universe at this early time. Up until this time the matter is strongly coupled to the radiation and will have the same temperature as the radiation; after it the matter decouples and can cool independently - and, eventually collapse under the effects of its own gravity and form stars and galaxies. A small amount of the matter will be reheated, up to temperatures as high as 107 in the subsequent evolution of matter, but as we saw in lecture 8, strong limits can be placed on the amount of such reheating because of the very small amount of inverse-Compton scattering measured in the microwave background photons.
The density evolution of matter and radiation are shown in the upper panel of figure 12.1, with the same divisions into radiation dominated and matter dominated eras marked.
|
Problem 12.4 Show that the density of matter and radiation are given by
and
When are these quantities the same for a present day mass density of rm,0 » 10-27 kg m-3 and present day radiation density of rt,0 » 4 ×10-31 kg m-3.
|
The scale factor, R(t) relative to the present radius of the Universe is just the redshift (since wavelength l µ R). This is usually denoted 1 + z.
| (21) |
The scale factor of the epoch separating the radiation and matter dominated universes is ~ 1000, which is also about the redshift of the surface of last scattering.
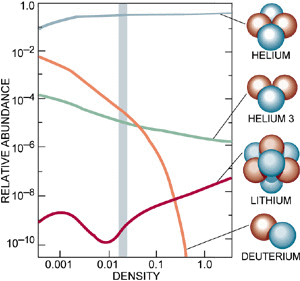
The previous section elaborates a model of the evolution of the Universe of astonishing simplicity. Its major success is that it provides a natural explanation for the microwave background. However, it can do plenty more! The next major success of the model is when we extrapolate back further in temperature to about 5 ×108 to 5 ×1010 K. At these temperatures, nuclear reactions can take place. The time interval after the Big Bang is about 0.05 sec to 500 sec, i.e. the famous ``first three minutes''. George Gamov has famously said of this time ``the elements were cooked in less time than it takes to cook a dish of duck and roast potatoes''. At smaller times, the nuclei produced are immediately photo-disintegrated, whereas afterwards the particle energies are too low to surmount the Coulomb barrier.
There is time to produce some Helium and light element nuclei. Everything else in he present Universe has been produced via nuclear reactions in the interiors of stars. The amount of light element might be expected to depend on the amount of neutrons and protons in the initial mix. Fortunately there is an interaction between the species which sets the number of each at the element building epoch. The relative quantities of each are related by their mass (energy) difference
| (22) |
where T is the temperature, and Dm ~ 1.29 MeV. This yields a ratio of about 0.2 at T ~ 1010 K. The neutrons would decay given time, but the temperature drops to T ~ 109 K after about 100 seconds, and nuclear reaction can take place.
| (23) |
| (24) |
| (25) |
| (26) |
| (27) |
| (28) |
This is about all that happens; nuclei with mass number 5 are not stable. Most of the neutrons end up in He4! The ratio of He to H nuclei is about 0.2×0.5 = 0.1, or about 10%. He thus occupies about 25% of the baryonic mass. This is just what is observed! Furthermore, similar processes predict a small amount of primordial Lithium, Li7, which turns out to be closed to te observed value of the baryonic density of matter is a few percent of the density of matter required to close the Universe.
| Site | Helium fraction (by mass) |
| Sun (at Birth) | 22-27 |
| Solar Cosmic Rays | 20-26 |
| Ancient stars (halo, globulars) | 20-30 |
| Planetary Nebulae | 40 |
| HII regions | ~ 27 |
Rather than continue to probe backwards beyond the generation of the light elements (in the first few minutes), let's run the story forwards. Some of these steps are illustrated in figure 12.3.
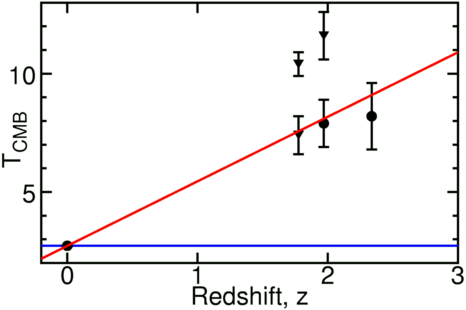
One of the key predictions of the Big Bang theory is that the temperature of the radiation should increase as we go backward in time, from the 2.7 K we see today. This can be tested by measuring certain C lines in distant gas clouds, which show up as absorption lines in the spectra of quasars. Recently, Srianand et al (2000) have shown that the strength of these lines is sensitive to the temperature of the background radiation. Such lines have been observed to redshifts of z ~ 2, when the microwave background was a toastier ~ 10 K (see figure 12.4).
Another test that the background radiation is present elsewhere in the cosmos comes from the Sunyaev-Zel'dovich effect, which we looked at in lecture 8. Cosmic background photons are slightly comptonised if they pass through a region of hot electrons in galaxy cluster halos. The effect has been observed in a handfull of clusters, but is very weak and rather challanging to measure. Nevertheless it supports the universiality of the microwave background.
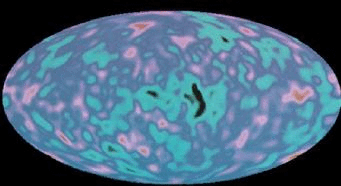
There are galaxies and stars in the Universe today, so we know that there must have been density fluctuations at early times, from which they formed via gravitational collapse. They key discovery in the 1990's, made by the COBE satellite, was the direct observation of these fluctuations on the microwave background. COBE detected perturbations of order 10-5 on scales greater than about 7 degrees, as shown in figure 12.5. These turned out to be just about what was expected, based on measurements of the structure which has formed since that time (i.e. the number and separation of galaxies on the sky).
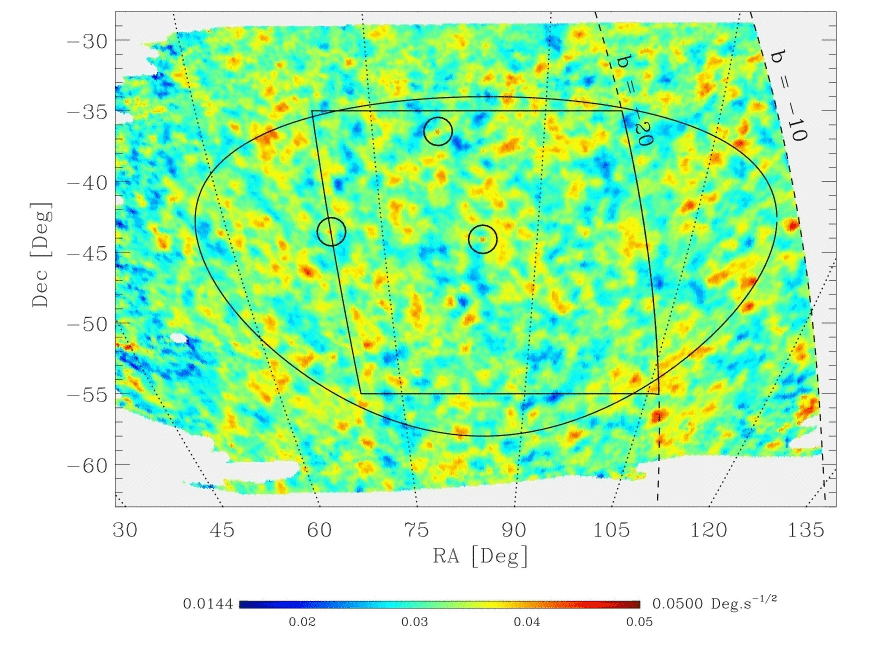
Since COBE, a great amount of follow up work has been carried out, with the aim of measuring the preturbations firstly at greater accuracy, but very importantly at much higher resolution (less than a degree). The reason is that various models of the amount of matter and energy in the Big Bang predict that the perturbations should cluster on different scales, but typically close to about 1 degree. A spectacular success came with the BOOMERANG mission, which flew on a balloon around the South Pole measuring the perturbations in a small area of sky. The flight time was about 260 hours and took place on Dec 29, 1998, flying at a height of about 40 km, with observations at 90, 150, 240 and 410 GHz. The map it produced is shown in figure 12.6.
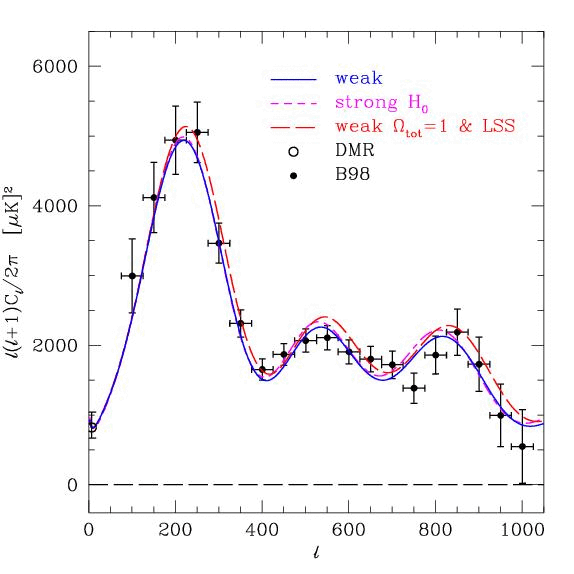
The angular power spectrum of the sources found by BOOMERANG is shown in figure 12.7. The plot shows the relative number of sources as a function of the angular separation on the sky, expressed as wave number l. Most sources are separated by about 0.5 degree (l ~ 200), but there are also secondary peaks in the spectrum at abpout l = 550 and l = 850. These are called accoustic peaks. They are the result of he detailed interaction of matter (which is beginning to act independently of radiation) and the radiation at recombination.
A typical over-density at this time might have an amplitude of dr/r = 1 ×10-4. Photons begin to cease interacting further with the matter as the electrons and atomic nuclei combine, and photons in an over-dense region will be redshifted (to lower energy) as the travel out of this region - the region will appear cooler relative to the average temperature. Similarly, under-dense regions will appear hotter, because the photons have had to do less work against the gravitational potential. The different regions have already begun the process of gravitational collapse, there are secondary effects to the main one of cooler and warmer regions as mapped by the photons. These manifest themselves as the accoustic peaks.
The position on the first peak was measured by Boomerang at l ~ 200: this is just where it is expected to be for a Universe model which is flat, and open, and contains an extra energy term in eqn 12.7 as a result of a very rapid phase of expansion at early times called inflation. The remarkable result is that the Universe is expected to expand forever, even if it has a critical density, because of the ``anti-gravity'' or repulsion caused by this extra term, L. The best fitting model of the Universe from these observtions, has about 30% of the energy in matter and 70% in a new form, called dark energy. The effect of this term is to cause the Universe to accelerate, particularly in the future. Its effect on the Einstein de-Sitter model we have been using so far has been only small for the Universe so far (15 Gyr).
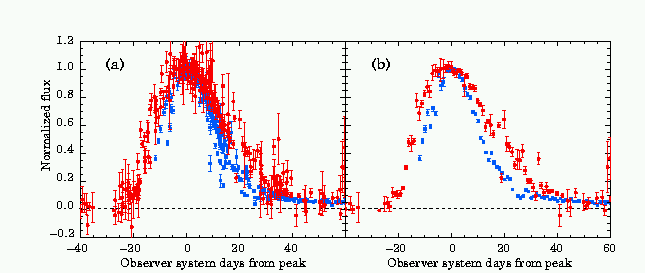
Another remarkable advance has taken place in recent years, through the search for and detection of very distant supernovae, up to redshifts of z ~ 2, although typically at z ~ 0.5. Supernovae of type SNIa have a well defined maximum light output and subsequent light decay time, as shown in figures 12.8 and 12.9.
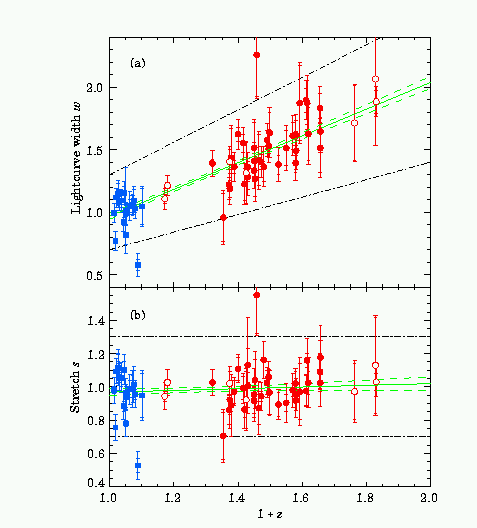
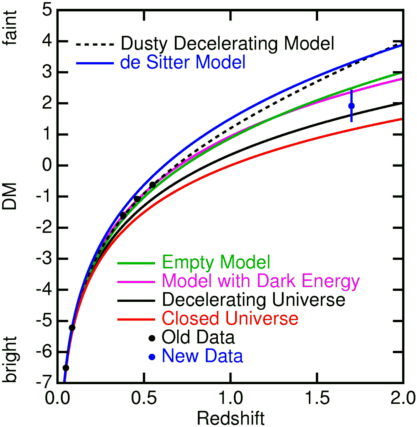
The distant supernova project was designed to test the expansion theory rigorously - because the absolute luminosity of these sources is known, their true distance can be determined and hence the rate of change of the scale of the Universe mapped out as a function of their redshift. The results were quite surpising - two groups found evidence for an accellerating Universe. This is just what the microwave background missions have found as well!
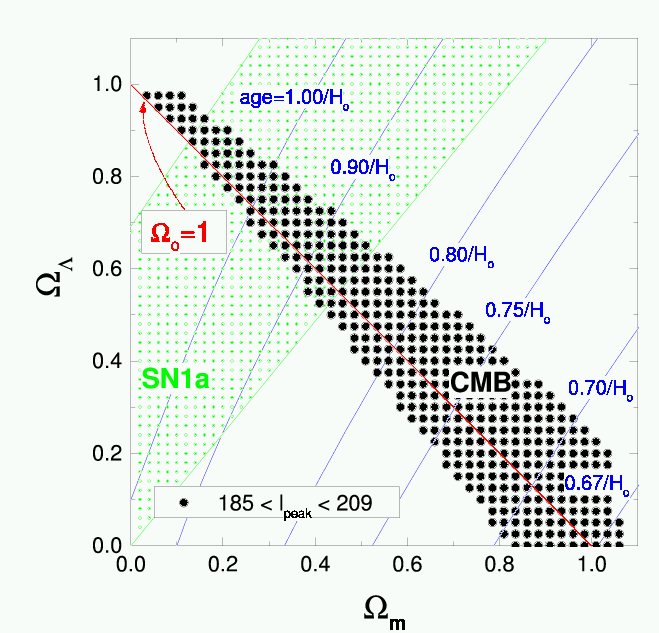
The two sets of results compliment each other very nicely, as shown in figure 12.11. Plotted are the density of matter in the Universe Wm versus the density of the dark energy WL. The black dots show the expected position of the first peak in the angular corellation spectrum (figure 12.7), while the green dots mark out the region consistent with the results of the high redshift supernovae. The red line marks W0 = 1, i.e. a universe with exactly the critical density. The best fit combination of these results is a Universe with Wm = 0.3 and WL = 0.7, and the Universe is precisely flat (actually, they measure W with an accuracy of about 5%.)
Inflation is a very special period in the early Universe when it expanded much faster than the rate predicted by models of the type discussed above. Inflation addresses several major problems in the big bang. The first of these is the flatness problem: why is the Universe so close to having a flat geometry? The second problem it addressed is called the horizon problem: why is the Universe so uniform on large scales? More information on this topic can be had from http://www.astro.ucla.edu/ wright/cosmo_04.htm.
www.damtp.cam.ac.uk/user/gr/public/bb_problems.html
www.physics.ucsb.edu/ boomerang/
www.physics.ucsb.edu/ boomerang/new_press_images/index.html
www.astro.ucla.edu/ wright/CMB-DT.html
www.astro.ucla.edu/ wright/cosmolog.htm
www.pbs.org/wnet/hawking/universes/html/univ.html