| kotisivu |
| hakemisto |
| kartat |
| kohteet |
| teoriaa |
| matematiikkaa |
| pallotähtitiede |
Pallokolmiot ovat pallon pinnalla olevia kuvioita, joita rajoittaa kolme isoympyrän kaarta. Pallokolmiolle voidaan johtaa joukko ratkaisukaavoja samaan tapaan kuin tasokolmiollekin. Helpoimmin niihin päästään käsiksi tutkimalla sopivia koordinaatistomuunnoksia.
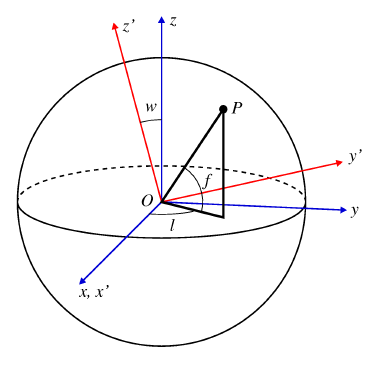 Tarkastellaan kahta suorakulmaista
koordinaatistoa Oxyz ja Ox'y'z'.
Oletetaan, että x'y'z'-koordinaatisto
saadaan xyz-koordinaatistosta kiertämällä sitä
x-akselin ympäri kulman w verran.
Tarkastellaan kahta suorakulmaista
koordinaatistoa Oxyz ja Ox'y'z'.
Oletetaan, että x'y'z'-koordinaatisto
saadaan xyz-koordinaatistosta kiertämällä sitä
x-akselin ympäri kulman w verran.
Origokeskisen yksikköpallon pinnalla olevan
pisteen P paikka voidaan ilmoittaa
suorakulmaisten koordinaattien lisäksi myös
kahden kulman avulla. Kulma l mitataan
positiivisesta x-akselista vastapäivään pitkin
xy-tasoa. Kulma f puolestaan
ilmoittaa pisteen kulmaetäisyyden tästä tasosta.
Vastaavalla tavalla voidaan määritellä kulmat
l' ja f', jotka ilmoittavat
pisteen paikan x'y'z'-koordinaatistossa.
Näiden kulmien avulla
lausuttuna pisteen P koordinaatit ovat
| x = cos l cos f | x' = cos l' cos f' |
| y = sin l cos f | y' = sin l' cos f' |
| z = sin f | z'= sin f' |

Toisaalta kysymyksessä on pelkkä koordinaatiston kierto yz-tasossa, joten pilkulliset koordinaatit saadaan pilkuttomista muunnoskaavoilla
x' = x,
y' = y cos w + z sinw,
z' = -y sin w + z cos w.
cos l' cos f' = cos l cos f,
sin l' cos f' =
sin l cos f cos w + sin f sin w,
sin f' =
-sin l cos f sin w + sin f cos w.
Itse asiassa näillä kaavoilla selvitäänkin jo kaikista tarvittavista koordinaatistomuunnoksista. Johdetaan kuitenkin vielä niiden avulla varsinaiset pallokolmion ratkaisukaavat, joissa esiintyy pelkästään pallokolmion sivuja ja kulmia.
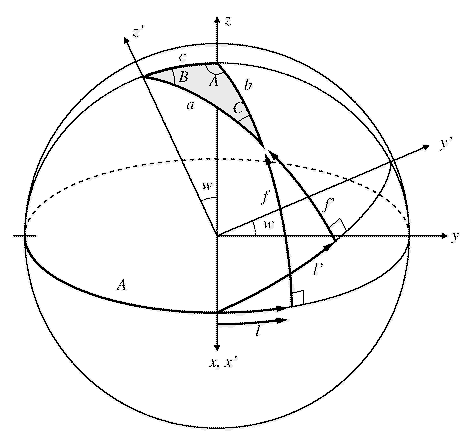
Tätä varten asetetaan koordinaatistot sopivalla tavalla pallokolmion ABC suhteen. Suunnataan z-akseli kolmion kärkeen A ja z'-akseli kärkeen B. Kärkipiste C vastaa nyt kuvan 2.4 pistettä P. Kulmat l, f, l', f' ja w voidaan lausua pallokolmion sivujen ja kulmien avulla seuraavasti:
l = A - 90°,
f = 90° - b,
l' = 90° - B,
f' = 90° - a,
w = c.
Sijoittamalla nämä yhtälöihin (2.5) saadaan
cos (90° - B) cos (90° - a) =
cos (A - 90°) cos (90° -b),
sin (90° - B) cos (90° - a) =
sin (A - 90°) cos (90° - b) cos c +
sin (90° - b) sin c,
sin (90° - a) =
-sin (A - 90°) cos (90° - b) sin c +
sin (90° - b) cos c
eli
sin B sin a = sin A sin b,
cos B sin a = -cos A sin b cos c +
cos b sin c,
cos a = cos A sin b sin c + cos b cos c
Muita sivuja ja kulmia koskevat kaavat saadaan vaihtamalla näissä syklisesti sivuja a, b, c ja kulmia A, B, C. Esimerkiksi ensimmäisestä kaavasta saadaan tällä tavoin yhtälöt
sin C sin b = sin B sin c,
sin A sin c = sin C sin a.
Kaikki nämä sinikaavan eri muodot voidaan kirjoittaa helposti muistettavaan muotoon:
sin a / sin A = sin b / sin B = sin c / sin C.
Jos annetaan sivujen a, b ja c pienentyä rajatta, pallokolmio lähenee tasokolmiota. Kun kulmat lausutaan radiaaneina, on pienille kulmille likimain
sin a = a,
cos a = 1 - a2/2.
Käyttämällä näitä approksimaatioita saadaan sinikaavan rajatapauksena tuttu tasokolmion sinikaava:
a / sin A = b / sin B = c / sin C.
Keskimmäinen ratkaisukaavoista on sini-kosinikaava, ja sen vastine tasokolmiolle on triviaali
c = b cos A + a cos B.
Tämä on saatu sijoittamalla ylläolevat sinin ja kosinin likiarvot sini-kosinikaavaan ja jättämällä pois kaikki toista astetta korkeammat termit. Samalla tavoin saadaan kolmannesta ratkaisukaavasta, eli kosinikaavasta, tasokolmion kosinikaava:
a2 = b2 + c2 - 2 bc cos A.
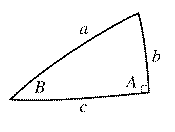 Olkoon pallokolmiossa kulma A suora.
Ratkaisukaavat tulevat silloin muotoon
Olkoon pallokolmiossa kulma A suora.
Ratkaisukaavat tulevat silloin muotoon
sin B sin a = sin b
cos B sin a = cos b sin c
cos a = cos b cos c
Ensimmäisestä yhtälöstä saadaan kulman B siniksi
sin B = sin b / sin a.
Jakamalla toinen ja kolmas yhtälö puolittain saadaan kulman B kosinille lauseke
cos B = tan c / tan a.
Ensimmäinen ja toinen yhtälö puolestaan antavat kulman B tangentin,
tan B = tan b / sin c.
Kolmas yhtälö on Pythagoraan teoreeman vastine suorakulmaiselle pallokolmiolle.
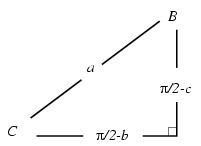
Usein hyödyllinen on myös Neperin sääntö. Suorakulmaisessa pallokolmiossa (A=pi/2) on ylläolevan kuvan kaavion kunkin suureen kosini = viereisten osien kotangenttien tulo = muiden osien sinien tulo:
cos C = cot a cot(pi/2-b)
= cot a tan b
= sin B sin(pi/2-c)
= sin B cos c,
cos a = cot B cot C
= sin (pi/2-c) sin(pi/2-b)
= cos c cos b,
cos B = cot(pi/2-c) cot a
= tan c cot a
= sin(pi/2-b) C = cos b sin C,
cos (pi/2-c) = sin c
= cot(pi/2-b) cot B
= tan b cot B
= sin C sin a,
cos (pi/2-b) = sin b
= cot C cot(pi/2-c)
= cot C tan c
= sin a sin B.